Ричард Фейнман - 5a. Электричество и магнетизм

§ 10. Поле внутри полости проводника

Вернемся теперь к проблеме пустотелого резервуара — про­водника, имеющего внутри полость. В металле поля нет, а вот есть ли оно в полости? Покажем, что если полость пуста, то поля в ней быть не может, какова бы ни была форма провод­ника или полости (фиг. 5.12). Рассмотрим гауссову поверхность, подобную S на фиг. 5.12, которая окружает собой полость, но остается всюду в веществе проводника. Всюду на поверхности S поле равно нулю, так что потока сквозь S быть не может, и суммарный заряд внутри S должен быть равен нулю. Затем можно вывести из симметрии, что на внутренней поверхности сферической оболочки нет никакого заряда. Но в более общем случае мы только можем сказать, что на внутренней поверх­ности проводника имеется равное количество положительного и отрицательного зарядов. Может быть, окажется, что на од­ной части имеется положительный заряд, а где-то в другом месте — отрицательный (см. фиг. 5.12)? Такие вещи законом Гаусса не исключаются.

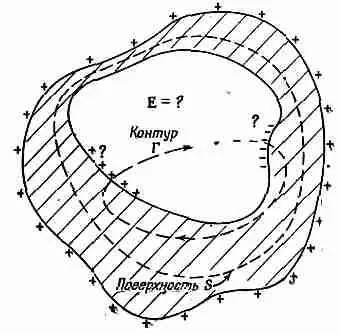
Фиг. 5.12. Чему равно поле в пустой полости проводника произвольной формы?

На самом деле, конечно, получается, что равные, но проти­воположные заряды на внутренней поверхности должны были бы соскользнуть навстречу друг другу и уничтожить друг дру­га. Мы можем убедиться в том, что они уничтожат друг друга, применив закон о равенстве нулю циркуляции Е (электроста­тику). Пусть на каких-то частях внутренней поверхности ока­зались заряды. Мы знаем, что еще где-то должно присутствовать равное количество противоположных зарядов. Но любые ли­нии поля Е начинаются на положительных зарядах и кончаются на отрицательных (мы рассматриваем случай, когда свобод­ных зарядов в полости нет). Представим себе теперь контур Г, пересекающий полость вдоль линии силы от какого-то положи­тельного заряда к какому-то отрицательному и возвращаю­щийся к исходной точке по телу проводника (см. фиг. 5.12). Интеграл вдоль такой линии сил в пределах от положительного до отрицательного заряда не был бы равен нулю, а интеграл по пути через металл

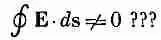
равен нулю, так как там Е = 0. Так что мы бы имели

Но криволинейный интеграл от Е по любому замкнутому кон­туру в электростатическом поле всегда равен нулю. Значит, внутри пустой полости не может быть никаких полей, равно как не может быть никаких зарядов на внутренней поверхности.

Заметьте, что мы все время подчеркивали, что полость пуста. Если поместить какие-то заряды в фиксированных местах по­лости (скажем, на изоляторе или на небольшом проводнике, изолированном от основного), то внутри полости могут быть поля. Но тогда она уже не будет «пустой».

Мы показали, что если полость целиком окружена провод­ником, то никакое статическое распределение зарядов снаружи никогда не создаст поля внутри. Это объясняет принцип «защи­ты» электрического оборудования, которое помещается в ме­таллическую коробку. К тем же рассуждениям можно прибег­нуть, если нужно показать, что никакое статическое распреде­ление зарядов внутри замкнутого сплошного проводника не может создать поля вне его. Защита действует в обе стороны! В электростатике (но не в изменяющихся полях) поля по обе стороны сплошной проводящей оболочки полностью не зависят одно от другого.

Теперь вы понимаете, почему удалось проверить закон Ку­лона с такой точностью. Форма полой оболочки не имела зна­чения. Она вовсе не должна была быть круглой, она могла быть и кубом! Если закон Гаусса точен, то поле внутри всегда равно нулю. Вы понимаете теперь, почему вполне безопасно сидеть внутри высоковольтного генератора Ван-де-Граафа в миллион вольт, не боясь, что вас ударит ток, — Вас охраняет сам Гаусс!

§1.Уравнения электростатиче­ского потенциала

§2.Электрический диполь

§3.3амечания о векторных уравнениях

§4.Дипольный потенциал как градиент

§5.Дипольное приближение для произвольного распределения

§6.Поля заряженных проводников

§7. Метод изображений

§8.Точечный заряд у проводящей плоскости

§9.Точечный заряд у проводящей сферы

§10.Конденеаторы; параллельные пластины

§11.Пробой при высоком напряжении

§12.Ионный микроскоп

Повторить: гл. 23 (вып. 2) «Резонанс»

§ 1. Уравнения электростатического потенциала

В этой главе мы расскажем о поведении электрического поля в тех или иных обстоятель­ствах. Вы познакомитесь с тем, как ведет себя электрическое поле, и с некоторыми математи­ческими методами, используемыми для опреде­ления поля.

Отметим для начала, что математически вся задача состоит в решении двух уравнений — максвелловских уравнений электростатики:

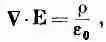
(6.1)

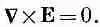
(6.2)

Фактически оба эти уравнения можно объ­единить в одно. Из второго уравнения сразу же следует, что поле может считаться гра­диентом некоего скаляра (см. гл. 3, § 7):

(6.3)

Электрическое поле каждого частного ви­да можно, если нужно, полностью описать с помощью потенциала поля j. Дифферен­циальное уравнение, которому должно удо­влетворять j, получится, если (6.3) подста­вить в (6.1):

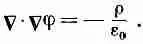
(6.4)

Расходимость градиента j—это то же, что С 2, действующее на j:

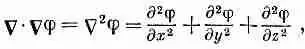
(6.5)

так что уравнение (6.4) мы запишем в виде

(6.6)

Оператор С 2называется лапласианом, а уравнение (6.6) — уравнением Пуассона. Весь предмет электростатики с мате­матической точки зрения заключается просто в изучении реше­ний одного-единственного уравнения (6.6). Как только из (6.6) вы найдете j, поле Е немедленно получается из (6.3).

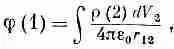
Обратимся сперва к особому классу задач, в которых r задано как функция х, у, z. Такая задача почти тривиальна, потому что решать уравнение (6.6) в общем случае мы уже умеем. Мы ведь показали, что если r в каждой точке известно, то потенциал в точке (1) равен