Ричард Фейнман - 5a. Электричество и магнетизм

(6.7)

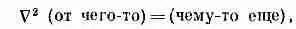
где r(2) — плотность заряда, dV 2— элемент объема в точке (2), а r 12— расстояние между точками (1) и (2). Решение диф­ференциального уравнения (6.6) свелось к интегрированию по пространству. Решение (6.7) нужно отметить особо, потому что в физике часто встречаются ситуации, приводящие к уравнениям, которые выглядят так:

и (6.7) является прототипом решения любой такой задачи.

Проблема расчета электростатического поля, таким образом, решается совершенно честно, если только положения всех за­рядов известны. Давайте посмотрим на нескольких примерах, как действует эта формула.

§ 2. Электрический диполь

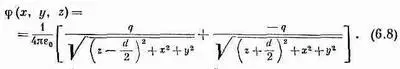
Сначала возьмем два точечных заряда + q и - q, разделенных промежутком d. Проведем ось z через заряды, а начало коор­динат поместим посредине между ними (фиг. 6.1). Тогда по фор­муле (4.24) потенциал системы двух зарядов дается выраже­нием

Мы не собираемся выписывать формулу для электрического поля, но всегда при желании можем это сделать, раз мы знаем потенциал. Так что задача двух зарядов решена.

Существует важный частный случай этой задачи, когда за­ряды расположены близко друг к другу, иными словами, когда нас интересует поле на таких расстояниях от зарядов, что по сравнению с ними промежуток между зарядами кажется незна­чительным. Такую тесную пару зарядов называют диполем. Диполи встречаются очень часто.

Фиг. 6.1. Диполь: два заряда +q и -q, удаленные друг от друга на расстояние d.

«Дипольную» антенну можно часто приближенно рассматривать как два за­ряда, разделенные неболь­шим расстоянием (если нас не интересует поле у са­мой антенны). (Обычно ин­терес представляют антенны с движущимися зарядами; уравнения статики тогда не­применимы, но для некоторых целей они все же представ­ляют весьма сносное приближение.)

Важнее, пожалуй, диполи атомные. Если в каком-то веще­стве есть электрическое поле, то электроны и протоны испыты­вают влияние противоположных сил и смещаются друг относи­тельно друга. Вы помните, что в проводнике некоторые электроны сдвигаются к поверхности, так что внутреннее поле обращает­ся в нуль. В изоляторе электроны не могут сильно разой­тись; им мешает притяжение ядра. И все же они как-то смеща­ются. Так что хотя атом (или молекула) и остается нейтральным, во внешнем электрическом поле все же возникает еле заметное разделение положительных и отрицательных зарядов, и атом становится микроскопическим диполем. Если нам нужно знать поле этих атомных диполей поблизости от предмета обычных размеров, то мы имеем дело с расстояниями, большими по срав­нению с промежутками между зарядами.

В некоторых молекулах из-за самой их формы заряды не­сколько разделены даже в отсутствие внешних полей. В моле­куле воды, например, имеется отрицательный заряд на атоме кислорода и положительный заряд на обоих атомах водорода, которые расположены несимметрично (фиг. 6.2). Хоть заряд всей молекулы равен нулю, все же имеется распределение за­ряда с небольшим преобладанием отрицательного заряда на од­ной стороне и положительного на другой. Это расположение, конечно, не такое простое, как у двух точечных зарядов, но если смотреть на него издалека, оно действует как диполь. Как мы увидим чуть позже, поле на больших расстояниях нечувстви­тельно к мелким деталям расположения.

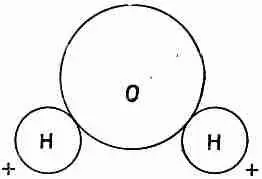
Фиг. 6.2. Молекула воды Н 2O.

Взглянем теперь на поле двух зарядов противоположных знаков, расстояние d между которыми мало. Если d станет ну­лем, два заряда сойдутся в одном месте, два потенциала сокра­тятся, поле исчезнет. Но если они не совсем слились, то можно получить хорошее приближение к потенциалу, разложив сла­гаемые в (6.8) в ряд по степеням малой величины d (по формуле бинома Ньютона). Оставляя только первые степени d, мы напи­шем

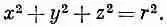
Удобно обозначить

Тогда

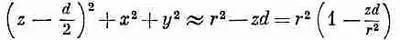
и

Разлагая в биномиальный ряд [1 — (zd/r 2)] -1/2и отбрасывая члены с высшими степенями d, мы получаем

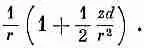
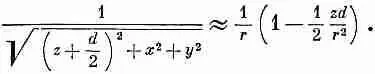
Подобно этому,

Вычитая эти два члена, имеем для потенциала

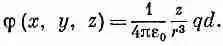
(6.9)

Потенциал, а значит, и поле, являющееся его производной, пропорциональны qd — произведению заряда на расстояния меж­ду зарядами.

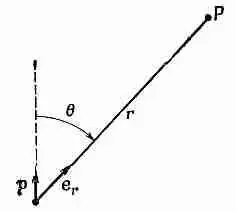
Фиг. 6.3. Векторные обозначения, для диполя.

Это произведение называется диполъным моментом пары зарядов, и мы обозначим его символом р (не путайте с импульсом!):

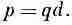
(6.10)

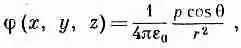
Уравнение (6.9) можно также записать в виде

(6.11)

так как z/r=cosq, где q — угол между осью диполя и радиус-вектором к точке (х, у, z) (см. фиг. 6.1). Потенциал диполя убы­вает как 1/r 2при фиксированном направлении (а у точечного заряда он убывает как 1/r). Электрическое поле Е диполя по­этому убывает как 1/r 3.

Мы можем записать нашу формулу и в векторном виде, если определим р., как вектор, абсолютная величина которого равна р, а направление выбрано вдоль оси диполя от q - к q + . Тогда

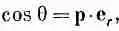
(6.12)

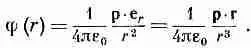
где е r— единичный радиальный вектор (фиг. 6.3). Кроме того, точку (x, y, z) можно обозначить буквой r. Итак, Дипольный потенциал: