Ричард Фейнман - 5a. Электричество и магнетизм
- Название:5a. Электричество и магнетизм
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 5a. Электричество и магнетизм краткое содержание
5a. Электричество и магнетизм - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
(8.27)
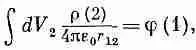
Обратите внимание на появление множителя 1/ 2. Он возник из-за того, что в двойном интеграле по dV 1 и по dV 2 каждая пара элементов заряда считалась дважды. (Не существует удобной записи интеграла, в которой каждая пара считалась бы только по одному разу.) Затем заметьте, что интеграл по dV 2в (8.27) — это просто потенциал в точке (1), т. е.
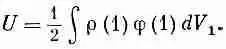
так что (8.27) можно записать в виде
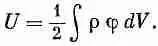
А так как точка (2) при этом выпала, то можно написать просто
(8.28)
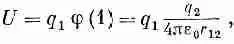
Это уравнение можно истолковать так. Потенциальная энергия заряда rdV равна произведению этого заряда на потенциал в той же точке. Вся энергия поэтому равна интегралу от jrdV. Но, кроме этого, есть множитель 1/ 2. Он все еще необходим, потому что энергии считаются дважды. Взаимная энергия двух зарядов равна заряду одного из них на потенциал другого в этой точке. Или заряду другого на потенциал от первого во второй точке. Так что для двух точечных зарядов можно написать
или
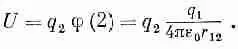
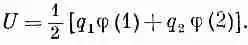
Обратите внимание, что это же можно написать и так:
(8.29)
Интеграл в (8.28) отвечает сложению обоих слагаемых в скобках выражения (8.29). Вот зачем нужен множитель 1/ 2.
Интересен и такой вопрос: где размещается электростатическая энергия? Правда, можно в ответ спросить: а не все ли равно?
Есть ли смысл у такого вопроса? Если имеется пара взаимодействующих зарядов, то их сочетание обладает некоторой энергией. Неужели нужно непременно уточнять, что энергия сосредоточена на этом заряде, или на том, или на обоих сразу, или между ними? Все эти вопросы лишены смысла, потому что мы знаем, что на самом деле сохраняется только полная, суммарная энергия. Представление о том, что энергия сосредоточена где-то, не так уж необходимо.
Ну а все же предположим, что в том, что энергия всегда сосредоточена в каком-то определенном месте (подобно тепловой энергии), действительно смысл есть. Тогда мы могли бы наш принцип сохранения энергии расширить, соединив его с идеей о том, что если в каком-то объеме энергия меняется, то это изменение можно учесть, наблюдая приток или отток энергии из объема. Вы ведь понимаете, что наше первоначальное утверждение о сохранении энергии по-прежнему будет превосходно выполняться, если какая-то энергия пропадет в одном месте и возникнет где-то далеко в другом, а в промежутке между этими местами ничего не случится (ничего — это значит не случится каких-либо явлений особого рода). Поэтому мы можем перейти теперь к расширению наших идей о сохранении энергии. Назовем это расширение принципом локального (местного) сохранения энергии. Такой принцип провозглашал бы, что энергия внутри любого данного объема изменяется лишь на количество, равное притоку (или убыли) энергии в объем (или из него). И действительно, такое локальное сохранение энергии вполне возможно. Если это так, то в нашем распоряжении будет куда более детальный закон, чем простое утверждение о сохранении полной энергии. И, как оказывается, в природе энергия действительно сохраняется локально, в каждом месте порознь, и можно написать формулы, показывающие, где энергия сосредоточена и как она перетекает с места на место.
Имеется и физический резон в требовании, чтобы мы были в состоянии указать, где именно заключена энергия. По теории тяготения всякая масса есть источник гравитационного притяжения. А по закону Е=тс 2 мы также знаем, что масса и энергия вполне равноценны друг другу. Стало быть, всякая энергия является источником силы тяготения. И если б мы не могли узнать, где находится энергия, мы бы не могли знать, где расположена масса. Мы не могли бы сказать, где размещаются источники поля тяготения. И теория тяготения стала бы неполной.
Конечно, если мы ограничимся электростатикой, то способа узнать, где сосредоточена энергия, у нас нет. Но полная система максвелловских уравнений электродинамики снабдит нас несравненно более полной информацией (хотя и тогда, строго говоря, ответ до конца определенным не станет). Подробнее мы этот вопрос рассмотрим позже. А сейчас приведем лишь результат, касающийся частного случая электростатики
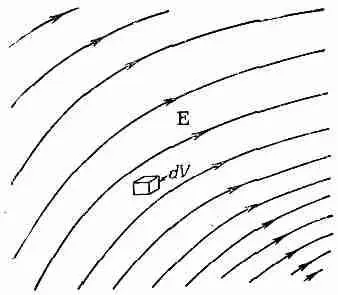
Фиг. 8.8. Каждый элемент объема dV=dxdydz в электрическом поле содержит в себе энергию (e 0/2) E 2 dV.
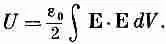
Энергия заключена в том пространстве, где имеется электрическое поле. Это, видимо, вполне разумно, потому что известно, что, ускоряясь, заряды излучают электрические поля. И когда свет или радиоволны распространяются от точки к точке, они переносят с собой свою энергию. Но в этих волнах нет зарядов. Так что энергию хотелось бы размещать там, где есть электромагнитное поле, а не там, где есть заряды, создающие это поле. Таким образом, мы описываем энергию не на языке зарядов, а на языке создаваемых ими полей. Действительно, мы можем показать, что уравнение (8.28) численно совпадает с
(8.30)
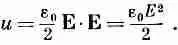
Эту формулу можно толковать, говоря, что в том месте пространства, где присутствует электрическое поле, сосредоточена и энергия; плотность ее (количество энергии в единице объема) равна
(8.31)
Эта идея иллюстрируется фиг. 8.8.
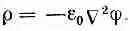
Чтобы показать, что уравнение (8.30) согласуется с нашими законами электростатики, начнем с того, что введем в уравнение (8.28) соотношение между r и j, полученное в гл. 6:
Получим
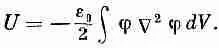
(8.32)
Расписав покомпонентно подынтегральное выражение, мы
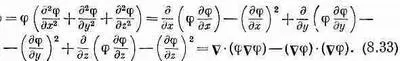
Интервал:
Закладка:





