Ричард Фейнман - 3a. Излучение. Волны. Кванты
- Название:3a. Излучение. Волны. Кванты
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 3a. Излучение. Волны. Кванты краткое содержание
3a. Излучение. Волны. Кванты - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Возникает вопрос, всегда ли при составлении смеси любого цвета входят три основных цвета с положительными коэффициентами? Нет, не всегда. Для каждой тройки основных цветов имеются цвета, для которых в смеси появляется отрицательный коэффициент, и поэтому однозначного способа выбора основной тройки не существует. В популярных книжках красный, зеленый и синий обычно называют основными цветами, но это объясняется только тем, что с их помощью можно создать более широкий набор цветов при положительных значениях коэффициентов в комбинации основных.
§ 4. Диаграмма цветности
Рассмотрим теперь смешивание цветов с математической точки зрения как некое геометрическое построение. Цвет, описываемый уравнением (35.4), можно представить вектором в трехмерном пространстве, где по трем осям отложены величины a, b и с, т. е. данному цвету соответствует точка в пространстве. Точка, соответствующая другому цвету, у которого компоненты равны а', b ' и с', расположена в другом месте.
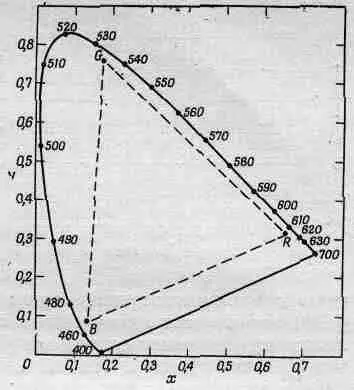
Фиг. 35.4. Стандартная диаграмма цветности.
Как мы уже знаем, сумма двух цветов есть новый цвет, который получается векторным суммированием первых двух. Диаграмму можно упростить и изобразить все на плоскости, если воспользоваться следующим наблюдением: возьмем свет определенной окраски и просто удвоим коэффициенты а, b и с, т. е. все компоненты увеличим, а соотношение между ними оставим неизменным; тогда получится свет той же самой окраски, но более яркий. Поэтому можно привести любой свет к одной и той же интенсивности и затем спроектировать все построение в трехмерном пространстве на плоскость, как это сделано на фиг. 35.4.
Отсюда следует, что любой цвет, полученный смешением двух заданных цветов, изображается точкой, лежащей на линии, которая соединяет оба выбранных цвета. Например, смесь, составленная из равных частей обоих цветов, лежит на середине соединяющего их отрезка; смесь из 1/ 4одного цвета и 3/ 4другого лежит на расстоянии 1 / 4длины отрезка и т. д.
Если в качестве основных цветов выбрать красный, зеленый и синий, то все цвета, получаемые из них с положительными коэффициентами, лежат внутри треугольника, изображенного на рисунке пунктиром. По существу, треугольник содержит почти все цвета, которые мы видим, поскольку вообще все цвета, доступные нашему зрению, заключены внутри кривой довольно странной формы, немного выступающей за треугольник. Откуда взялась эта кривая? Кто-то когда-то весьма тщательно составил смеси всех видимых цветов из трех выбранных. Но мы не будем проверять все цвета; достаточно исследовать лишь чистые спектральные тона, линии спектра.
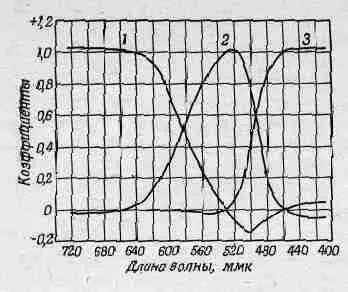
Фиг. 35.5. Цветовые коэффициенты чистых спектральных тонов для некоторого выбора основных цветов. 1 — красный; 2 — зеленый; 3 — синий.
Любой цвет можно рассматривать как сумму чистых спектральных тонов с различными, но положительными коэффициентами (чистых с физической точки зрения). Любой цвет состоит из некоторых количеств красного, желтого, синего и т. д. по всем цветам спектра. Зная, как составлены спектральные тона из трех основных цветов, можно вычислить необходимую пропорцию основных цветов и для какого угодно цвета. Поэтому, определив цветовые коэффициенты всех спектральных тонов по отношению к трем основным цветам, легко составить полную таблицу смешения цветов.
В качестве примера на фиг. 35.5 приведены опытные данные по смешению трех цветов. Кривые показывают количество каждого из трех основных цветов (красного, зеленого, синего), образующих при смешении любой из цветов спектра. Красный цвет расположен на левом конце спектра, следом идет желтый цвет и т. д. до синего цвета, расположенного на правом краю. Заметьте, что в некоторых случаях необходимо брать отрицательные коэффициенты. Именно из таких данных и были определены положения точек для всех цветов на диаграмме, причем координаты х и у связаны с относительными количествами основных цветов, использованных для получения различных цветов. Отсюда же была найдена и граничная кривая диаграммы. Она представляет собой геометрическое место всех чистых спектральных тонов. Но каждый цвет может быть получен смешением спектральных тонов, поэтому любой цвет на линии, соединяющей две произвольные точки кривой, существует в природе. На диаграмме прямая соединяет крайний фиолетовый и далекий красный концы спектра. На ней расположены пурпурные цвета. Внутри кривой находятся те цвета, которые могут быть получены с помощью света, а цвета вне кривой вообще не могут быть созданы светом, и никто их никогда не видел (разве только во сне!).
§ 5. Механизм цветового зрения
Первый вопрос, который возникает по поводу изложенных закономерностей: почему цвета ведут себя таким образом?
Простейшая теория, предложенная Юнгом и Гельмгольцем, предполагала, что глаз обладает тремя сортами пигментов, восприимчивых к свету, и что спектры поглощения этих пигментов разные, скажем, один сильно поглощает красный свет, другой — синий, а третий — зеленый. Поэтому когда свет попадает в глаз, поглощение в каждой из трех областей происходит по-разному, а, исследуя разную поступающую информацию, наш мозг, или глаз, или еще что-то решает, какой цвет попал в глаз. Легко показать, что из предположения о трех сортах пигментов вытекают все правила смешения цветов.
Дальше, казалось бы, оставалось определить кривые поглощения всех трех пигментов, но по этому поводу возникли серьезные разногласия. К несчастью, оказалось, что можно найти только всевозможные линейные комбинации кривых поглощения, а не сами кривые для каждого пигмента в отдельности, потому что координаты на диаграмме могут быть повернуты любым образом. Пробовали использовать самые разные пути для получения кривых, характеризующих отдельные физические свойства глаза. Одна из таких кривых, называемая кривой яркости, представлена на фиг. 35.3.
На рисунке показаны две кривые: одна для глаза, адаптированного к темноте, а другая для зрения на свету (последняя характеризует зрение с помощью колбочек). Кривая указывает наименьшую яркость света данной окраски, которую еще способен воспринять глаз, т. е. характеризует чувствительность глаза в разных областях спектра.
Существует другой, очень интересный способ измерения этой же величины. Возьмем два цвета и будем попеременно показывать их на экране. Тогда, если частота их появления достаточно мала, мы увидим на экране мелькание. С увеличением частоты мелькание в конце концов исчезнет. Это произойдет при некоторой частоте, зависящей от яркости света и равной, скажем, 16 повторениям в секунду. Теперь можно так подобрать яркости, или интенсивности, двух цветов относительно друг друга, чтобы мелькание цвета при 16 циклах исчезало. При установленной яркости мелькание цветов возникает, только если перейти к меньшей частоте. Следовательно, при большой частоте мы получаем так называемое мелькание яркости, а при меньших частотах — мелькание цвета. Таким способом удается подобрать два цвета с «одинаковой яркостью». Получающиеся отсюда результаты почти, но не совсем аналогичны данным по пороговой чувствительности глаза к слабым потокам света, наблюдаемым с помощью колбочек. Большинство специалистов
Читать дальшеИнтервал:
Закладка:



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/1068056/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov.webp)

