Александр Филиппов - Многоликий солитон

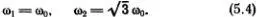
*) Если хотя бы в один момент времени y 1 0, то множитель в квадратных скобках, не зависящий от времени, должен обращаться в нуль.

Если ω = ω 1, то из уравнений (5.2) следует, что y 2= y 1. Если ω = ω 2, то y 2= - y 1. Вспомним теперь, что y 1и y 2подчиняются уравнениям 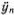= -ω 2 y n , которые определяют их гармоническую зависимость от времени. При ω = ω 1= ω 0можно поэтому записать решение в виде

y 1= y 2= А 1cos [ω 1( t - t 1)], (5.5а)

а при ω = ω 2= 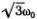— в виде

y 1= - y 2= А 2cos [ω 2( t - t 2)]. (5.5б)

Здесь A 1и А 2— произвольные амплитуды, а t 1и t 2— произвольные значения времени, определяющие фазу колебаний.

Эти два решения и дают две возможные моды колебаний нашей простейшей системы (рис. 5.4).

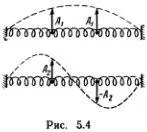
Они соответствуют двум нашим модам колебаний резинки, изображенным на рисунке штриховыми линиями. Конечно, это соответствие несколько условно, но, согласитесь, от карикатуры, сделанной двумя точками, нельзя требовать большего! Теперь можно снова воспользоваться линейностью уравнений (5.1) и написать решение в виде суммы решений (5.5а) и (5.5б):

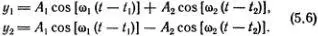
Это движение уже не сводится к простому гармоническому колебанию каждой из частиц. В общем случае, т. е. при произвольных значениях А 1, А 2, t 1, t 2, движение системы не будет даже периодическим.

Упражнение : рассмотрите простой случай, когда А 1= А 2= 1, t 1= t 2= 0, и покажите, что из-за несоизмеримости частот ω 1 и ω 2не существует такого значения Т , при котором y 1( Т ) = y 1(0), y 2( Т ) = y 2(0). Это и означает, что такое движение не может быть периодическим.

Ясно, что формулы (5.6) дают самое общее движение. Начальное состояние определяется координатами и скоростями частиц, т. е. значениями y 1(0), y 2(0), 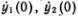. Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А 1, А 2, t 1, t 2через начальные координаты и скорости.

Замечательно, что нам удалось не только найти самое общее движение, но и разложить его на сумму самых простых из известных нам движений.

Конечно, в такой простой задаче то же самое можно было бы сделать и более простым способом. Например, если сложить и вычесть уравнения (5.1), то легко получить два независимых уравнения для ( y 1 + y 2) и ( y 1 - y 2), которые сразу решаются и приводят к формулам (5.6).

Однако наш чуть более длинный способ решения имеет преимущество — он легко обобщается на случай цепочки с любым числом частиц.

В качестве упражнения найдите частоты трех мод колебаний цепочки, состоящей из трех частиц. Для частот должен получиться результат: 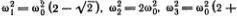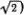. Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде

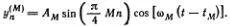
При заданном М = 1, 2, 3 индекс n пробегает три значения: n = 1, 2, 3, т. е. 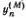задает отклонение n-гo грузика в М -й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде

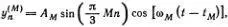
где М = 1, 2 и n = 1, 2.

Общую закономерность теперь нетрудно уловить и она наглядно ясна — нарисованные штрихами синусоиды соответствуют стоячим волнам. Легко также догадаться, что в цепочке из N частиц моду с номером М надо искать в виде

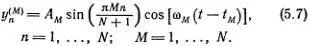
Уравнение движения для n -гo атома составляется точно так же, как уравнения (5.1), т. е.

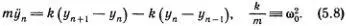
Это уравнение годится и для крайних атомов — первого и N -гo. Нужно только вспомнить, что крайние пружинки закреплены, т. е. у 0= y N +1= 0. Эти условия для предполагаемых решений (5.7) уже выполнены. Теперь должно быть ясно, как довести решение до конца. Надо подставить выражение (5.7) в уравнение (5.8) и заменить 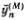на -ω 2 My n (М). После несложных преобразований тригонометрических функций получится соотношение для ω 2 M , при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода

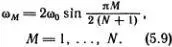
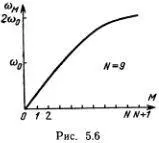
Эта зависимость частоты от номера моды изображена на рис. 5.6. Для мод с малыми номерами (низкочастотных и длинноволновых) частота пропорциональна номеру моды. Для высокочастотных мод (коротковолновых) частота выходит на предельное значение 2ω 0.

Формула (5.9) определяет спектр частот собственных колебаний (мод) цепочки. Не удивительно, что в цепочке из N частиц имеется ровно N собственных частот. Нетрудно понять и происхождение предельной частоты. Если один из грузиков колеблется слишком быстро, то соседние не успевают реагировать на его движение, и возбуждение не сможет распространяться вдоль цепочки. Этот вывод легко проверить, проделав простые опыты.

Читателю стоит потратить некоторое время, чтобы самостоятельно разобраться в этих результатах. Затраченные усилия полностью окупаются. После уравнений Галилея — Ньютона и принципа сохранения энергии разложение произвольного движения на моды, или нормальные колебания, представляет собой, возможно, самой фундаментальный результат физики. Его обобщения и приложения, от простых механических задач до современных проблем физики элементарных частиц, просто невозможно перечислить.