Александр Филиппов - Многоликий солитон

Он показал, каким образом можно найти движение струны по начальным значениям отклонений и скоростей точек струны (в математике эта задача и называется задачей Коши ). Он также связал решения волнового уравнения, полученные методами Д'Аламбера и Фурье, доказав полную справедливость принципа суперпозиции, и даже попытался объяснить дисперсию света в веществе, считая, что свет возбуждает упругие волны с очень высокой частотой. Коши очень ясно показал, что при длинах волн, много больших расстояний между частицами в цепочке, скорость распространения волн в цепочке не зависит от длины волны, т. е. нет дисперсии. Для коротких же волн скорость зависит от длины волны и может заметно изменяться. Это полностью справедливо для упругих волн, но дисперсию световых волн объясняет лишь качественно. Более точную модель дисперсии света нашел, как уже упоминалось, Кельвин.

Понимание связи между ньютоновской дискретной средой (от лат. discгetus — прерывистый, разделенный) и эйлеровой непрерывной средой очень важно, так как в разных случаях удобно переходить от дискретного языка к непрерывному и обратно.

Например, если изучаются упругие волны в кристаллах, то обычно можно забыть об их атомной структуре и считать кристалл просто непрерывной упругой средой. Атомная структура скажется на том, что упругие свойства кристалла будут разными в разных направлениях. Мы, однако, пойдем намеченным путем, так как у нас есть надежные уравнения (5.8), описывающие движения каждой точки дискретной системы.

Предположим для определенности, что грузопружинная модель, изображенная на рис. 5.1, должна приближенно воспроизводить продольные колебания и волны в упругом стержне. Точно так же можно рассмотреть звуковые волны в трубе, поперечные колебания струны и т. п. Идея перехода к непрерывной среде ясна: нужно уменьшать массы грузиков и длины пружинок так, чтобы средняя линейная плотность (т. е. масса на единицу длины ρ 1= m/α) и упругость пружины оставались постоянными.

Сначала надо немного точнее определить, что такое упругость пружины. В правой части уравнения (5.8) написана сила, действующая на n -й грузик при растяжении n -й пружины с длиной α на величину Δ l : F = k ( y n+1- y n) = k Δ l . Значение коэффициента k должно подбираться так, чтобы стержень и пружинная система одинаковой длины растягивались на одну и ту же величину под действием одной и той же силы.

Удлинения стержня и пружины пропорциональны их длине. Например, если пружинка удлиняется на Δ l , то обе ее половинки удлиняются на Δ l /2. Это значит, что коэффициент k для пружинки длиной α/ 2 равен просто 2 k . Поэтому, записав силу F = k Δ l в виде F = kα( Δ l/α) , мы получим характеристику упругости пружины, не зависящую от ее длины: для пружины любой длины α величина kα = К одна и та же. Для стержня любой длины l также будет верно соотношение F = К( Δ l/l ). Значение К определяется только упругостью стержня и не зависит от его длины.

Уравнение (5.8) легко переписать так, чтобы оно зависело лишь от ρ 1= m / α и К = kα , а не от m и k . После этого можно показать, что для волн, длина которых много больше α , можно при достаточно малых значениях α описать распространение волн в стержне уравнением Д'Аламбера

Движение каждой частицы стержня определяется, если известно решение у ( t, х ) этого уравнения: у n ( t ) = y (t, x = nα ). Скорость распространения упругих волн по стержню очевидно равна 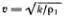. В качестве упражнения попробуйте «вывести» уравнение (5.12) из уравнения (5.8).

Скорость распространения волн по цепочке можно найти, и не прибегая к уравнению Д'Аламбера. Если по цепочке бежит волна неизменной формы со скоростью v , то она перемещается на расстояние α за время Δ t = α / v .

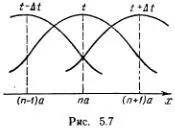
Отсюда следует, что y n-1( t ) = y n( t + Δ t ) и y n+1( t ) = y n( t - Δ t ) (рис. 5.7). Если рассматривать y n( t ) как график движения некоторой точки, то 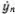( t ) будет скоростью, а 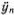( t ) — ускорением точки. Приближенно считая движение от момента t - Δ t до момента t + Δ t равномерно ускоренным, можно написать

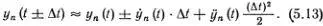
Подставляя полученные таким способом выражения для y n-1( t ) и y n+1( t ) в уравнение (5.8), находим, что [ m - k (Δ t ) 2] 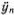( t ) = 0. Отсюда следует, что (Δ t ) 2= m/k (предполагается, конечно, что в какой-нибудь момент времени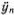 0). Для скорости волны v = α /Δ t находим поэтому выражение

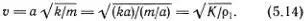
Чтобы найти скорость распространения упругих волн (т. е. скорость звука) в реальных твердых телах, надо еще немного преобразовать формулу . В таком виде она, на первый взгляд, зависит не только от вещества, из которого изготовлен стержень, но и от его поперечного сечения S . Действительно, линейная плотность равна произведению обычной объемной плотности ρ на поперечное сечение: ρ 1= ρ • S . Однако упругая постоянная К численно равна силе, необходимой для увеличения длины стержня в два раза ( F = К (Δ l/l ) = К , если Δ l = l ; при реальном измерении К , естественно, рассматривается лишь малое относительное удлинение Δ l/l и К определяется как отношение силы F к вызванному ею относительному удлинению). Ясно, что эта сила пропорциональна площади S , и поэтому К = Е • S, где величина Е уже не зависит от S , а определяется лишь материалом, из которого сделан стержень.

Эту постоянную Е называют модулем Юнга. Значения модуля Юнга и объемной плотности для различных материалов измерены на опыте, и их можно найти в справочниках. Например, для стали ρ = 7,8 г / см 3, Е 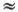2,1 • 10 12г/(см • с 2). Выражая ρ 1 и К через ρ и Е , находим скорость звука в стали v = 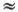5 км/с. Это неплохо согласуется с прямыми измерениями.