Александр Филиппов - Многоликий солитон

Подумайте, как их можно было бы осуществить. Ясно, что легче измерять не скорость, а длину волны 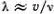. При 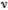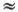10 кГц получаем λ 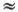50 см.

До конца XVIII в. думали, что звук в твердых телах передается мгновенно. Первое измерение скорости звука в твердых телах по отношению к скорости в воздухе выполнил в 1797 г. немецкий ученый Эрнст Хладни (1756—1827). Он же провел первые точные и тщательные измерения скорости звука в различных газах, пользуясь для этой цели органными трубами. Хладни получил юридическое образование, а естественные науки изучал самостоятельно. Под влиянием чтения сочинений Бернулли и Эйлера он заинтересовался акустикой и начал изучать звучащие пластинки, в результате чего открыл прославившие его «звуковые фигуры» *). Фигуры Хладни образуются на посыпанных песком колеблющихся пластинках (песок собирается в узлах стоячих волн).

*) Первым сумел сделать звуковые колебания «видимыми» Галилей. Он поместил бокал в воду так, чтобы края его немного выступали над поверхностью. При возбуждении в бокале звуковых колебаний около него на поверхности образуется радиальная рябь поверхностных волн.

Хладни также открыл продольные и вращательные колебания в стержнях, открыл и изучил многие акустические колебательные явления, изобрел несколько музыкальных инструментов, на которых сам играл. Его опыты, всегда отличавшиеся изобретательностью и остроумием, заложили основы экспериментальной акустики, и ему принадлежит первое систематическое изложение акустики, выпущенное в свет в 1802 г. Под впечатлением обаяния личности Хладни, его лекций и опытов, Наполеон выделил 6000 франков для перевода его «Акустики» на французский язык.

Скорость распространения звуковых волн можно оценить и просто из соображений размерности. Так как механизм распространения волн нам уже достаточно понятен, нетрудно сообразить, что скорость звука в стержне зависит лишь от модуля Юнга Е, плотности ρ и, может быть, от длины волны λ: v = d• Е аρ Ьλ с. Так как [ Е ] = ML -1 Т -2, [ρ] = ML -3, [λ] = L и [ v ] = LТ -1, то а = -b = 1/2, с = 0, т. е. v = d , где d — неизвестное число (как показано выше, из формулы (5.14) следует, что d = 1).

Любопытно, что простые соображения размерности показали, что скорость звука не может быть пропорциональна какой-нибудь степени. Это значит, что дисперсию (т. е. зависимость скорости от длины волны) из простых соображений размерности получить нельзя. Заметим также, что мы не учли зависимость v от амплитуды колебаний. Это представляется разумным для малых амплитуд, когда эффектами нелинейности можно пренебречь (ср. с формулой (4.1)).

При отсутствии дисперсии из соображений размерности следует независимость скорости звука от амплитуды. Проверьте это, предположив, что в формуле размерности для v показатель с = 0, но введя зависимость от амплитуды.

Точно так же можно оценить скорость звука в жидкостях, например в воде. Только в этом случае вместо модуля Юнга надо взять модуль объемной упругости жидкости К . Он определяется соотношением Δ p = K (Δ V/V ), где Δ p — приращение давления, необходимое для того, чтобы уменьшить объем V на величину Δ V . Эта формула совершенно аналогична соотношению F/S = E (Δ l/l ) для стержня, и мы сразу можем найти скорость звука в жидкостях: 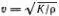. для воды ρ = 1 г/см 3, К 2,13•10 10г/(cм•c 2), так что v 1460 м/с. Заметьте, что скорость звука зависит от плотности, а значит, несколько меняется с температурой.

Между прочим, до начала XIX в. распространение звука в жидкостях считалось невозможным. Хладни придерживался противоположного мнения, но попыток измерить скорость звука в жидкостях не делал. Первое измерение было выполнено в год смерти Хладни швейцарскими учеными Жаном Колладоном и Жаном Штурмом, получившими значение v = 1435 м/с при температуре 8 0С.

Читатель легко найдет и скорость распространения поперечных волн в натянутой струне. В этом случае возвращающая сила пропорциональна силе натяжения струны F , и при малом изгибе и растяжении струны не зависит от ее упругости. Предполагая, что v = dF aρ l Ь, где ρ l— линейная плотность струны, покажите, что 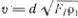; из опыта и из более полной теории следует, что d = 1. Это соотношение в равной степени применимо к металлической струне, нитке и рыболовной леске.

Опыты удобнее всего делать с леской. Изменяя ее натяжение, можно менять частоту основного тона, который можно отождествить с одной из нот, извлекаемых на фортепиано. Нота «ля» первой октавы обычно настраивается с помощью камертона на частоту 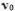= 440 Гц. Частоты 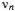, соответствующие другим нотам, определяются соотношением log( 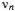/ 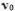) = (n/12)log2. Для «ля» во второй октаве n = 12 и частота равна 2 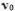. При ходе от 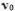на октаву ниже n = -12 и частота равна 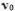/2.

Определяя частоты с помощью фортепиано или другого музыкального инструмента, можно найти скорость распространения волны по формуле v = λ 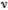, так как длина волны основной моды для струны с закрепленными концами равна удвоенной длине струны. Пользуясь этой простой идеей, Хладни и определил на опыте скорости звука в газах и твердых телах, только частоты он определял не на фортепиано, а на монохорде. Хорда в переводе с древнегреческого — струна, и монохорд можно назвать «однострунником». Это просто струна на резонаторе, длину звучащей части которой можно менять. Монохорд, вероятно, изобрел Пифагор. Он же первым открыл простые соотношения между музыкальными интервалами.

Легко найти и скорость звука в газах. Аналог модуля упругости в этом случае — давление. Действительно, из закона Бойля—Мариотта pV = const следует, что V •Δ p + p •Δ V = 0, т. е. Δ p = - p (Δ V/V ). Подставляя в формулу для скорости звука в жидкости вместо модуля объемной упругости давление, находим 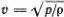. Эту формулу получил Ньютон, который пользовался описанной в начале этой главы дискретной моделью. Рассуждения Ньютона были весьма сложны и стали понятны лишь после работ Бернулли, Эйлера и Лагранжа. Лагранж писал: «эта теория одними почиталась за непонятную, другие находят ее противоречивой, в сущности же, если она и обладает каким недостатком, то тем, что она слишком частная, но вместе с тем она содержит зачаток истинной теории, открытой лишь в последнее время при помощи анализа».