Александр Филиппов - Многоликий солитон

В предельном случае, когда пружинки очень мягкие, дислокация ФК превращается в «дырку» по Френкелю.

*) Такие движения называют «асимптотическими», имея в виду, что график движения приближается к прямой, соответствующей положению равновесия, подобно тому как гипербола приближается к своей асимптоте.

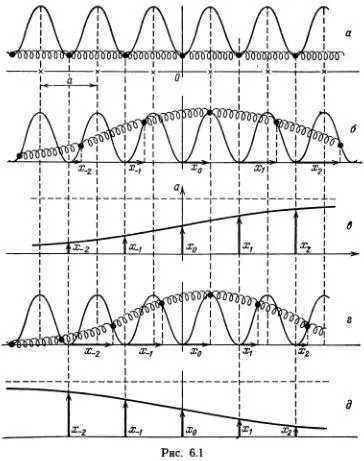
На рис. 6.1, б и в изображена дислокация, в которой вблизи точки О «меньше» атомов, чем в недеформированном состоянии (рис. 6.1, α ). Может случиться так, что вместо этого образуется «сгущение» атомов, как изображено на рис. 6.1, г и д . График смещений атомов в такой дислокации также соответствует асимптотическому движению маятника, но в обратном направлении. В предельном случае мягких пружин получается состояние, в котором одна ямка содержит лишний атом.

На самом деле понятие дефекта по Френкелю включает пару — дырку и ячейку с лишним атомом. Их можно считать как бы «частицей» и «античастицей», родившимися в тот момент, когда один из атомов перескочил в соседнюю ячейку. Эта пара может разойтись, и тогда можно говорить отдельно о «дырке» или «сгущении». Точно так же и распределенные дефекты-дислокации могут порождаться и уничтожаться парами. Дислокацию разрежения условимся называть «положительной» или просто дислокацией . Дислокацию сгущения назовем «отрицательной» или антидислокацией .

Дислокация, размер которой значительно превышает шаг решетки α , свободно перемещается. Чтобы сдвинуть всю дислокацию на расстояние α , нужно сместить каждый атом на относительно малую длину; при этом нужно затратить совсем немного энергии. Таким образом, дислокации могут перемещаться по кристаллу как частицы, не изменяя свою форму. Разумеется, это относится к идеальным системам, когда все горбики и ямы одинаковы, а грузики и пружинки также не отличаются друг от друга. Если, однако, один горбик заметно выше других, то ясно, что дислокация будет как бы «отталкиваться» от него и сможет проскочить эту неоднородность только при достаточно большой скорости движения. Наоборот, более низкий, чем другие, горбик будет «притягивать» к себе дислокации. К похожим эффектам могут привести и неоднородности в пружинах и массах гpyзиков.

Немного поразмыслив, можно понять, что одна дислокация действует на другую как неоднородность. Точнее, две положительные или две отрицательные дислокации как бы «отталкиваются» друг от круга, а положительная и отрицательная — «притягиваются». Притяжение дислокации и антидислокации — вещь довольно очевидная, так как в дислокации пружины растянуты, а в антидислокации сжаты. Столь же очевидна причина отталкивания «одноименных» дислокаций. Психологически легче понять, как отталкиваются две антидислокации, в которых пружинки сжаты. Однако дислокации отталкиваются точно так же.

Из всего, что пока было сказано, вовсе не очевидно, что такие равновесные конфигурации, как показанные на рис. 6.1, б или г , существуют. Могло бы случиться и так, что при всяком отклонении грузиков от равновесных положений по цепочке просто бегут волны. Именно так обстоит дело в обычной ньютоновой цепочке (рис. 5.1), в струне и в других одномерных системах. На самом деле точно так же «распадаются» на волны и все достаточно малые начальные отклонения в модели ФК. Все дело здесь именно в «достаточной малости». Действующие на грузики силы тяжести и натяжения пружин могут уравновешиваться только при больших смещениях атомов. Если каким-то способом создать вначале достаточно большое смещение атомов, скажем, перебросить один или несколько атомов в соседние ямки, то в результате по цепочке побегут волны сжатия и разрежения. Оказывается, что когда мелкие волны убегут далеко, останется некоторое количество дислокаций и антидислокаций, которые сравнительно медленно движутся или покоятся.

Таким образом, любое начальное возмущение «распадается» на бегущие волны и несколько дислокаций и антидислокаций. Их форма не зависит от начального возмущения, а определяется лишь параметрами модели (массами грузиков, жесткостью пружин, формой волнистой поверхности).

Без достаточно сложных математических расчетов невозможно понять, что будет происходить с двумя дислокациями, сталкивающимися друг с другом. Точное решение уравнений показывает, что одноименные дислокации взаимодействуют точно так же, как солитоны Рассела, т. е. подобно сталкивающимся мячам (см. рис. 2.4). Попробуем если и не понять, то хотя бы описать, что происходит, когда на покоящуюся антидислокацию налетает другая антидислокация. Обе дислокации во время «соударения» несколько деформируются. За время их соприкосновения кинетическая энергия налетевшей дислокации перейдет к первоначально покоившейся, которая и начнет двигаться вперед, сохраняя свою форму. В общем, можно сказать, что дислокация подобна мячу. Главное здесь то, что дислокация сохраняет форму. Ее легче сдвинуть, чем деформировать.

На самом деле, как мы скоро увидим, дислокация не деформируется лишь при малой скорости ее движения, много меньшей скорости распространения продольной звуковой волны по цепочке атомов. В общем случае все продольные (по оси, соответствующей направлению движения) размеры дислокации уменьшаются, т. e. 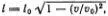где v — скорость дислокации, v 0— скорость распространения звука. Зависимость энергии движущейся дислокации от скорости дается формулой 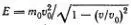. Как формула для размеров дислокации, так и формула для энергии аналогичны соответствующим формулам специальной теории относительности *). C учетом всего, что мы узнали о дислокациях, можно сказать, что дислокация подобна элементарной частице. В довершение этой поразительной аналогии, имеются еще и «античастицы» — антидислокации.

*) Нелишне подчеркнуть, что эта аналогия чисто математическая. В теории относительности написанные формулы имеют совершенно другой физический смысл. К тому же, для реальных дислокаций они выполняются лишь приближенно.

Как же происходит столкновение дислокации с антидислокацией? Когда антидислокация (антисолитон) 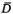налетает слева на покоящуюся дислокацию D (солитон), то сжатые в 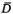пружины распрямляются, из 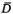в D пробегает волна сжатия, которая превращает D в 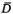, и наоборот. Все эти события происходят очень быстро, так как передача энергии от 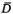к D и распространение волны сжатия, превращающей D в 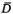и 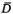в D , происходят со скоростью звука. Если начальная скорость налетающего солитона намного меньше скорости звука, то оба солитона не успеют заметно изменить свою форму и разлетятся, как мячи. В результате налетевший антисолитон 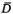превратился в солитон D и остановился несколько левее положения первоначально покоившегося солитона D . Тот, в свою очередь, превратился в антисолитон 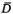и летит направо, занимая положение немного правее того, которое занимал бы налетающий антисолитон, если бы не было столкновения. Таким образом, мы совершенно ясно видим, что ничего похожего на прохождение одного солитона «сквозь другой» не происходит. Только на первый взгляд может показаться, что солитоны ведут себя как импульсы в струне, движение которых мы изучали в гл. 5.