Александр Филиппов - Многоликий солитон

Для понимания соотношения между полем и солитоном, напротив, не требуется никакой квантовой теории, и я постараюсь больше не вспоминать ни о каких квантах. Давайте действительно вернемся к солитонам. Я покажу, как основные свойства солитона Френкеля можно получить на точном языке математики. При этом Вы увидите, что все опять сводится к движению маятников, точнее, к асимптотическим движениям маятника (вспомните рис. 4.14). Надеюсь, Вы еще не забыли, что это такое?

Ч и т а т е л ь. Признаться, я не очень внимательно прочел главу о маятнике. Она мне показалась слишком длинной. К тому же я не понимаю, как Вы хотите связать дислокацию с маятником. Понятно, что каждую частицу в ямке можно считать маятником. Однако когда дислокация стоит на месте, грузики неподвижны, речь, по-моему, может идти не о колебаниях, а о равновесии маятников, связанных пружинами... Впрочем, если дислокация движется, то грузики действительно ведут себя как маятники, делающие одно полное колебание. Только почему оно асимптотическое?

А в т о р. Я мог бы ответить на этот вопрос, но давайте лучше сначала уточним модель и напишем некоторые формулы.

Признаюсь, что я пока немного обманывал Вас, выдавая за модель Френкеля — Конторовой более наглядную, но и более сложную систему. Теперь займемся настоящей моделью Френкеля — Конторовой.

Если Вы хотите по-настоящему понять, как устроен хотя бы один солитон, попробуйте разобраться в следующих двух параграфах, возвращаясь время от времени к формулам, описывающим маятник и движения грузиков в пружинной модели. Если у Вас нет желания заниматься этой работой, можно бегло просмотреть эти параграфы. Советую все же постараться понять, что изображено на рис. 6.3 и 6.4 и обратить внимание на закон дисперсии волн в модели Френкеля — Конторовой.

В настоящей модели ФК атомы, естественно, движутся по прямой (ось х ) и все силы, действующие на них, направлены также по оси х . Действие соседних атомов верхнего слоя представим, как всегда, пружинами, а действие атомов нижнего слоя («подкладки») описывается периодической синусоидальной силой

f ( х ) = - f 0sin (2π x/α ).

Как и в предыдущей главе, обозначим отклонение n- го атома от положения равновесия функцией y n ( t ) = x n ( t ) - nα , где x n ( t ) — координата n -го атома. Со стороны «подкладки» на n -й атом действует сила

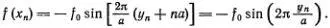
Пружины действуют на n-й атом с силой, равной

k ( y n+1 - y n ) - k ( y n - y n-1 ).

Уравнение движения n -го атома поэтому принимает вид

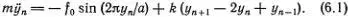
Если f 0= 0, то мы получаем уравнение (5.8), уже изученное раньше.

Итак мы получили уравнение (6.1), соответствующее модели Френкеля — Конторовой. Сейчас мы найдем решение этого уравнения, описывающее движущуюся дислокацию. Читателя, разобравшегося в предыдущей главе, уже не смущает что это не одно уравнение, а бесконечная система уравнений. Мы знаем что движущаяся дислокация подобна волне, бегущей по цепочке маятников, в которой каждый маятник с некоторым запаздыванием точно повторяет все движения предыдущего. Время этого запаздывания Δ t определяется скоростью перемещения волны v = α/ Δ t . Таким образом (вспомните рис. 5.7)

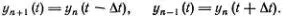
Смещения y n ( t + Δ t ) можно найти, считая движение атома от момента t - Δ t до момента t + Δ t равномерно ускоренным. Тогда, как мы уже писали,

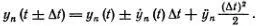
Подставляя это в уравнение (6.1), получаем замечательно простое уравнение

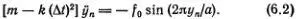
Присмотримся к этому уравнению повнимательнее. Если отвлечься от обозначений, то видно, что оно почти совпадает с уравнением маятника, о котором так много говорилось в гл. 4. Когда периодической силы не было, т. е. f 0= 0, мы должны были положить m = k (Δ t ) 2, откуда и определили скорость распространения звука в свободной цепочке:

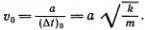
Теперь квадратная скобка не равна нулю. Перепишем ее в виде

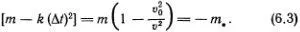
Теперь ясно, что при медленном движении дислокации, когда v 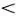v 0, квадратная скобка отрицательна, а определенная нами эффективная масса m •, зависящая от скорости v , положительна.

Легко свести уравнение (6.2) к уравнению маятника (4.1). Вспомним, что sin (π + φ) = -sin φ, и положим 2π( y n / α ) = π + φ n , т. е. будем измерять отклонение атома от положения равновесия «углом» φ n . Если атом остался на месте, то y n = 0 и φ n = -π. Если он смещается вправо, то угол φ n возрастает и при y n = α принимает значение +π. Таким образом, переходу атома со дна одной «ямки» на дно другой соответствует асимптотическое движение «маятника». При таком изменении обозначений уравнение движения (6.2) можно записать в виде (проверьте это!)

Движение «маятника» по сепаратрисе, когда φ n ( t ) изменяется от -π до +π, мы уже определили раньше (вспомним формулу (4.9) и рис. 4.10). Напишем эту формулу еще раз:

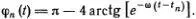
Так как маятники качаются с запаздыванием, мы выбрали свое начало отсчета времени t n для каждого из маятников. Поскольку смещение атомов от ячейки к ячейке распространяется со скоростью v = α/ Δ t , надо взять t n = n Δ t . Тогда φ 1( t ) = φ 0( t - Δ t ), и вообще φ n ( t ) = φ 0( t - n Δ t ).

Выразим теперь t n через скорость дислокации, т. е. t n = nα• (Δ t /α) = nα / v , и заменим nα на х . Будем писать соответственно φ n ( t ) = φ( t , х ), где х = nα . Тогда функцию φ( t , х ), описывающую движущуюся дислокацию, можно записать в виде

φ( t , х ) = π - 4 arctg [ e - ω( t - x/v )].