Александр Филиппов - Многоликий солитон
- Название:Многоликий солитон
- Автор:
- Жанр:
- Издательство:Наука, гл. ред. физ.-мат. лит.
- Год:1990
- Город:Москва
- ISBN:5-02-014405-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Филиппов - Многоликий солитон краткое содержание
Одно из наиболее удивительных и красивых волновых явлений — образование уединенных волн, или солитонов, распространяющихся в виде импульсов неизменной формы и во многом подобных частицам. К солитонным явлениям относятся, например, волны цунами, нервные импульсы и др.
В новом издании (1-е изд. — 1985 г.) материал книги существенно переработан с учетом новейших достижений.
Для школьников старших классов, студентов, преподавателей.
Многоликий солитон - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Будем теперь пропускать через вещество короткие импульсы длительностью, скажем,  10 -10с и с несущей частотой
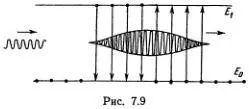
10 -10с и с несущей частотой  10 15Гц (эта частота как раз и соответствует условию резонанса). Оказывается, что при достаточно большой амплитуде импульсов среда внезапно становится прозрачной для них! Что происходит? Приблизительно вот что. Передний фронт импульса перебрасывает электроны на верхний уровень и ослабляется, а задний фронт возвращает их в прежнее состояние, причем возникающее при этом излучение возвращается импульсу. В то же время скорость импульса и его форма «подстраиваются» так, что все эти процессы происходят совершенно синхронно (рис. 7.9). Оказывается, что форму импульса можно найти, решив уравнение, по существу совпадающее с уравнением ФК, хотя этот импульс представляет собой типичный групповой солитон (модулированная волна). В частности, его скорость и ширина зависят от амплитуды.
10 15Гц (эта частота как раз и соответствует условию резонанса). Оказывается, что при достаточно большой амплитуде импульсов среда внезапно становится прозрачной для них! Что происходит? Приблизительно вот что. Передний фронт импульса перебрасывает электроны на верхний уровень и ослабляется, а задний фронт возвращает их в прежнее состояние, причем возникающее при этом излучение возвращается импульсу. В то же время скорость импульса и его форма «подстраиваются» так, что все эти процессы происходят совершенно синхронно (рис. 7.9). Оказывается, что форму импульса можно найти, решив уравнение, по существу совпадающее с уравнением ФК, хотя этот импульс представляет собой типичный групповой солитон (модулированная волна). В частности, его скорость и ширина зависят от амплитуды.
Естественно использовать подобные оптические солитоны для передачи информации по оптическим волокнам. Выгоды такого способа — большая скорость передачи очень большого количества информации (за счет малой длительности импульса), малый расход энергии и высокая надежность. В недалеком будущем нам с вами, вероятно, представится возможность пользоваться таким «солитонным телеграфом»!
Солитонный телеграф
В то время когда были написаны слова о солитонном телеграфе (в конце 1984 г.), японский физик, сотрудник лабораторий Белла в США Акира Xacегaвa опубликовал подробные численные расчеты распространения солитонов в оптических волокнах и показал, что оптические солитоны могут пробегать тысячи километров без серьезного искажения их формы. Весной 1988 г. этот вывод был полностью подтвержден на опыте сотрудниками лабораторий Белла Л. Молленауэром и К. Смитом, которым удалось четко детектировать солитоны, пробежавшие более четырех тысяч километров. Эти солитоны несколько отличаются от других оптических солитонов, и сам «солитонный телеграф» основан на несколько необычной идее применения солитона. Мы сейчас с ней познакомимся, но начнем несколько издалека.
Как только (лет 1З назад) появились световоды достаточно хорошего качества, естественно возникла идея применить их для передачи информации оптическими импульсами. Из-за малой длины световых волн можно передавать гораздо большие объемы информации. Такой способ передачи оказывается также весьма дешевым. В результате оптические системы передачи замечательно быстро начали входить в жизнь. В середине этого десятилетия оптическая связь была установлена между крупнейшими городами Японии, а в США — между Бостоном, Нью-Йорком и Вашингтоном. Прокладываются линии между восточным и западным побережьями США. В 1988 г. начинает работать трансатлантическая оптическая связь. Планируется прокладка кабеля через Тихий океан. Одно волокно пропускает сотни мегабит в секунду. Кабель, состоящий из многих волокон, может пропускать несколько гигабит. Это очень хорошо. Однако потенциальные возможности пропускной способности оптических волокон несоизмеримо выше! Что же ограничивает оптический телеграф?
В любом, даже самом качественном световоде сигнал постепенно слабеет и расплывается. Поэтому через каждые 50—100 км ставится приемник, который образует оптические сигналы в электронные (детектирует), усиливает их, вновь превращает в оптические и посылает дальше. Такие электронные регенераторы могут пропускать до одного гигабита в секунду, тогда как пропускная способность световода могла бы быть раз в сто больше. Кроме этого, использование многих регенераторов увеличивает возможность ошибок и отказов. Короче говоря, нужно что-то более простое и фундаментальное.
Естественно, мысль обращается к оптическим солитонам. Если в световоде распространяется достаточно мощный импульс, созданный лазером, то начинает проявляться зависимость показателя преломления от амплитуды импульса. Эта зависимость определяется поляризацией молекул электрическим полем светового импульса. Зависимость показателя преломления света от внешнего электрического поля была открыта еще в 1875 г. шотландским физиком Джоном Керром (1824—1907) и называется эффектом Керра . Добавка к показателю преломления пропорциональна квадрату напряженности электрического поля. Чтобы наблюдать этот эффект, нужно создать сильное электрическое поле (примерно десять тысяч вольт/см). Так как в волнах света, испускаемых обычными источниками, напряженность электрического поля не превышает сотни вольт/см, то эти волны не могут заметно поляризовать молекулы, и нелинейностью показателя преломления всегда можно пренебречь. Другое дело — лазерный свет. Напряженность электрического поля в нем может достигать ста миллионов вольт/см, а это уже сравнимо с электрическими полями внутри молекул.
Такая зависимость показателя преломления приводит к замечательному явлению — самофокусировке лазерного луча . Обычно световой луч в стекле постепенно расширяется. Однако достаточно мощный лазерный луч в некоторых видах стекол может, наоборот, сфокусироваться в тонкую ниточку. Качественно это объясняется тем, что показатель преломления оказывается наибольшим на оси пучка света и, согласно обычному закону преломления, боковые лучи будут искривляться и «притягиваться» к оси. Точная теория этого явления, однако, довольно сложна, и впервые была построена В. И. Захаровым и А. Б. Шабатом в работе «Точная теория двумерной самофокусировки и одномерной автомодуляции волн в нелинейных средах» (1971 г.). Распространение света в нелинейной среде описывается так называемым нелинейным уравнением Шрёдингера , точно такому же уравнению удовлетворяют солитоны огибающей, описанные выше. Отсюда сразу следует, что в нелинейной среде могут распространяться такие же солитоны.
В 1973 г. А. Xacегaва и Ф. Тапперт применили нелинейное уравнение Шрёдингера к распространению лазерного света в световоде и нашли условия, при которых их можно было бы наблюдать. В 1980 г. эти солитоны наблюдали Л. Молленауэр, Р. Столен и Дж. Гордон. В их опытах солитоны пробегали почти километр без заметного искажения формы. Однако если мы хотим, чтобы солитонные сигналы можно было бы принимать на очень больших расстояниях, нужно как-то компенсировать потерю их энергии. Заметим, что скорость солитонов не зависит от их энергии, но высота уменьшается, а ширина увеличивается (их произведение постоянно).
Читать дальшеИнтервал:
Закладка:










