Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Формулируя этот постулат, мы снова не стремились к безупречной строгости. Мы просто пытались, пусть грубо и неполно, отметить опытный факт: «Если в Москве имелось два равных стержня, то один из них можно провезти по всему свету так осторожно, что, вернувшись в Москву, мы найдем после окончания движения, что стержни остались равными».

Используя определение длины и этот постулат, можно утверждать, что если стержень A тождественно равен стержню B , а стержень B — стержню C , то A = C , то есть можно сравнивать длины тел, пребывающих в покое относительно друг друга, но удаленных один от другого на большое расстояние. Это, впрочем, уже тонкости.

Пожалуй, стоит отметить вот какую сторону вопроса. Несколько раньше мы уже сетовали, что в отличие от математиков физики имеют дело с реальными объектами и должны помнить о реальных физических свойствах. Так вот, постулат, по существу, утверждает, что длина физического стержня, участвующего по крайней мере в некоторых видах движения, остается постоянной (и в этом он ничем не отличается от масштабного отрезка), то есть после окончания движения он остается таким же, как и до начала.

Значит, имея определение длины, дополненное постулатом № 1, можно совершенно точно измерять и сравнивать длины неподвижных относительно друг друга предметов [8] .

Но пока мы не владеем никаким другим методом определения длины, кроме прикладывания к измеряемому предмету масштаба, и не знаем по-прежнему, как определять длину предмета, который двигается относительно масштабного стержня.

С первой трудностью можно разделаться сразу.

Чтобы измерить длину предмета, неподвижного относительно эталона длины, мы можем воспользоваться любым методом определения длины, разрешенным геометрией, например методом триангуляции, без которого были бы совершенно немыслимы точные геодезические измерения. Идея триангуляции очень проста и, конечно, многим знакома.

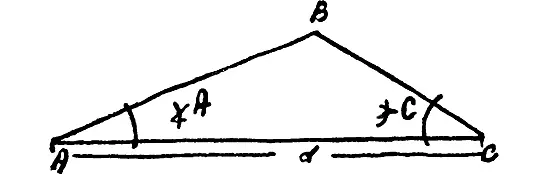
Допустим, нужно измерить отрезок AB . Тогда под произвольным углом к AB строим отрезок AC — базу, — длину которого точно определяем, откладывая масштаб. После этого измеряем угол A и угол C . Узнав их, мы однозначно определим ABC и, использовав формулы тригонометрии, можем вычислить длину AB .

Таким путем, имея базу АС , скажем, зная расстояние между двумя кремлевскими башнями, можно совершенно точно определить расстояние до шпиля университета ( AB ), не занимаясь утомительным, а часто и невозможным откладыванием масштаба. Полезно помнить, между прочим, что геодезические измерения вообще немыслимы без применения триангуляции.

Но для нас интересно другое. Для измерения длины AB использовался физический процесс, совершенно отличный от процесса измерения длины, данного в определении. Мы не откладывали вдоль AB масштаб, а привлекли измерение углов. Можно ли было утверждать заранее, что длина AB , полученная методом триангуляции, совпадает с длиной AB , измеренной откладыванием масштаба? Не есть ли «триангуляционная длина» AB нечто отличное от «нормальной длины»? Ведь мы использовали два совершенно различных рецепта измерения. Заранее, конечно, мы не могли ожидать такого совпадения.

Однако, вспомнив, что теоремы геометрии доказывают равенство результатов измерения длины путем триангуляции и откладыванием масштаба, а также зная, что в окружающем мире соблюдается наша геометрия [9] , мы заключаем, что «нормальная» и «триангуляционная» длины совпадают.

Описывает ли наша геометрия окружающий мир или нет — решает опыт. Если, используя в расчетах геометрию Эвклида, мы получили бы при триангуляции другие результаты, чем при откладывании масштаба вдоль прямой AB , то должны были бы заключить, что в мире осуществляется какая-то другая, неэвклидова геометрия.

Все, что сказано о методе триангуляции, конечно, относится и к любому другому процессу определения длины, опирающемуся на геометрию.

Итак, зная геометрию мира (и сведя к ней вопрос об измерении длины), мы сразу овладеваем бесчисленным числом рецептов измерения длины, ибо геометрические теоремы доказывают, что все они тождественны основному рецепту — «откладыванию масштаба».

Приведем теперь краткое резюме. Вот что сделано.

Дано определение понятия длины, заимствованное у математиков. Из определения вытекает, что для измерения длины необходимо иметь выбранный по соглашению вполне реальный эталон длины — масштабный стержень.

Введен постулат, который мог показаться весьма туманным. Но он был необходим, чтобы в вопросах измерения длины неподвижных относительно измерителя тел полностью опираться на геометрию.

Вскользь отмечено, что только опыт показывает, какая геометрия описывает наш мир.

Было установлено, что все рецепты измерения длины неподвижных тел сводятся благодаря геометрии к основному рецепту — откладыванию масштаба.

И в результате… не получено как будто ничего нового.

Мало того, предложенный рецепт измерения не подходит для измерения длины тел, движущихся относительно наблюдателя. Довольно точно, хотя несколько вульгарно, это можно пояснить так: «К движущемуся предмету масштаб не приложить: измеряемый предмет просто-напросто уедет».

Казалось бы, возможно использовать многочисленные косвенные способы измерения, подобные, например, триангуляции. Однако если детально проанализировать все мысленные возможности, окажется, что все способы определения длины движущегося тела в конечном итоге сводятся к следующему рецепту-определению:

Чтобы измерить длину стержня, двигающегося относительно наблюдателя, необходимо одновременнозафиксировать начальную и конечную точки измеряемого стержня на предмете, неподвижном относительно наблюдателя.

После этого откладыванием масштаба измерить расстояние, которое получилось на нашем «неподвижном предмете». Эта длина и есть длина движущегося стержня .

Если выражаться не так учено, то все сводится к следующему.

Вы стоите, скажем, на платформе железнодорожной станции, снабженные всеми мыслимыми измерительными приборами. Мимо вас едет поезд, длину которого необходимо измерить. Тогда вы: