Вольдемар Смилга - Очевидное? Нет, еще неизведанное…
- Название:Очевидное? Нет, еще неизведанное…
- Автор:
- Жанр:
- Издательство:Молодая гвардия
- Год:1966
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Вольдемар Смилга - Очевидное? Нет, еще неизведанное… краткое содержание
Эффектное название, возможно, и интригует, но, уж конечно, ничего не объясняет. А в этой книге довольно серьезно рассказывается о том, чего достигла физика со времен Галилея до Эйнштейна, о явлениях древних, как мир, и, по-видимому, всем знакомых, а в конечном счете — о специальной теории относительности.
Очевидное? Нет, еще неизведанное… - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Казалось бы, после Эйнштейна в физике не должно остаться места подобным взглядам. Но, как ни парадоксально, основные споры, которые ведутся вокруг трактовки теории относительности, возникают именно в результате необдуманного употребления слов без ясного понимания их содержания.
Глава XIII,
Несколько упрощая, можно заявить: вся математическая сторона теории Эйнштейна основана на одном факте — инвариантности интервала.
Что такое «интервал» и его «инвариантность», сейчас скажем. Правда, в нашей беседе значение понятия интервала не будет раскрыто, и, уверяя читателя, что это очень важно, автор напоминает человека, демонстрирующего фотографию тигра, чтобы доказать, какой это страшный зверь. У собеседника же всегда останется смутное подозрение, что перед ним просто увеличенный портрет котенка. Тем не менее от соблазна продемонстрировать фото все же трудно удержаться…
Инвариантность интервала и чуть-чуть математики.Пусть произошли два каких-то события А и В .
Пусть координаты этих событий, измеренные в определенной инерциальной системе отсчета K , — x A; y A; z Aи x B; y B; z B.
Пусть, наконец, определенные в той же инерциальной системе моменты времени, когда случились эти события, — t Aи t B.
Тогда интервал между этими событиями определяется соотношением:
S 2 AB = c 2( t B – t A) 2 – ( x B – x A) 2 – ( y B – y A) 2 – ( z B – z A) 2.
И эта величина обладает замечательным свойством.
Допустим, что наши события А и В рассматривают из другой инерциальной системы отсчета K 1. Обозначим координаты событий в этой новой системе x 1 A; y 1 A; z 1 Aи x 1 B; y 1 B; z 1 B, а моменты времени, когда произошли события, — t 1 Aи t 1 B. Для наглядности снова представим некую многострадальную железную дорогу — такую, что система отсчета, связанная с полотном дороги, инерциальна. Допустим, это система К . (Если вспомнить, что система отсчета «Земля», строго говоря, неинерциальная, наш рельсовый путь придется проложить где-то в космосе.)
Пусть по дороге равномерно и прямолинейно идет поезд. Тогда система отсчета, связанная с поездом, тоже инерциальна. Это система K 1. Где-то на небосклоне вспыхнули две звезды — это события А и В .
Если наблюдатели на полотне дороги и в поезде отметят координаты событий и моменты, когда они произошли, то окажется, что
S AB = S 1 ABили c 2( t B – t A) 2 – ( x B – x A) 2 – ( y B – y A) 2 – ( z B – z A) 2 = c 2( t 1 B – t 1 A) 2 – ( x 1 B – x 1 A) 2 – ( y 1 B – y 1 A) 2 – ( z 1 B – z 1 A) 2.
Интервал между событиями неизменен при переходе от одной инерциальной системы к другой. Иначе говоря — интервал инвариантен.
Предыдущее равенство еще удобнее записать так:
S 2 AB = c 2 t 2 AB – r 2 AB = c 2( t 1 AB) 2 – ( r 1 AB) 2 = ( S 1 AB) 2.
Вот что такое инвариантность интервала.Здесь r ABи r 1 AB— расстояние между точками, где произошли события A и B в системах K и K 1, а t ABи t 1 AB— соответственно промежутки времени.
Как установили, что интервал остается неизменным, инвариантным при переходе от одной системы к другой?
Инвариантность интервала — просто математическая запись основных положений теории — принцип относительности плюс принцип постоянства скорости света. Как именно доказывается инвариантность интервала, обсуждать не стоит, хотя это и довольно просто. Это вопрос математики, а математика, как говорил А. Н. Крылов, подобно мельнице, перемалывает все, что вы засыплете. Нас же интересует в первую очередь «засыпка».
Из инвариантности интервала немедленно следуют преобразования Лоренца — формулы, позволяющие перейти от одной инерциальной системы отсчета к другой.
Это тоже математика. Опустим вывод преобразования Лоренца и даже скрепя сердце промолчим об удивительно изящной математической трактовке этих преобразований, принадлежащей Минковскому. В конце концов все это относится к работе мельницы, а нам с лихвой хватит попытки разобраться в основных физических выводах теории. Посему все формулы будем принимать на веру.
1. Рассмотрим две инерциальные системы отсчета K и K 1, оси которых по направлениям совпадают.
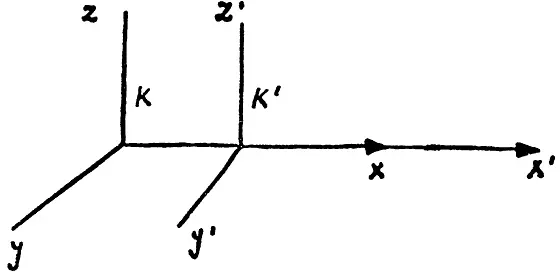
Пусть относительная скорость движения этих систем v направлена вдоль осей x и x 1 . Тогда, зная время и координаты любого события в одной системе отсчета, можем найти время и координаты этого же события в другой системе. А именно:
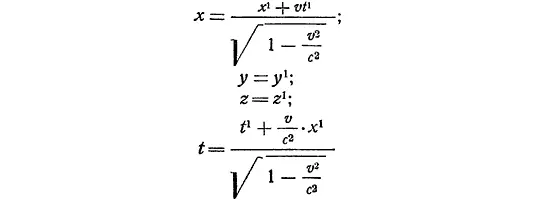 Эти формулы и определяют преобразование Лоренца.
Эти формулы и определяют преобразование Лоренца.
Как видите, написаны формулы перехода от штрихованной системы к нештрихованной [69] .
Из рисунка видно, что рассматривается случай, когда скорость системы K 1в системе K равна + v .
Теперь, зная координаты и время в системе K 1и использовав наши формулы, сразу можем найти соответствующие координаты и время в системе K .
Чтобы проделать обратный переход, нужно разрешить наши уравнения относительно x 1и t 1(как говорится, «уединить» x 1и t 1). Это очень легко сделать чисто формально, но еще проще вспомнить, что ввиду равноправия инерциальных систем формулы перехода от K к K 1и от K 1к K должны иметь тождественный вид.
Учитывая, что скорость движения K относительно K 1равна — v , сразу напишем:
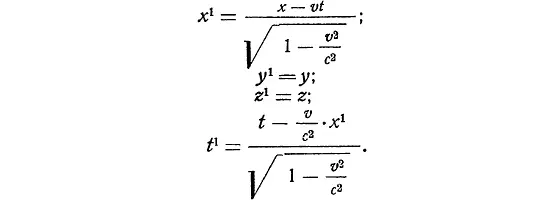
Мы рассмотрели сравнительно простой случай, когда относительная скорость движения систем K к K 1совпадает по направлению с осями x и x 1.
В общем случае формулы перехода, естественно, усложняются, но все принципиальные отличия теории Эйнштейна от классической физики полностью выявлены и в частном случае.
Сразу видно, как существенно отличаются преобразования Лоренца от аналогичного преобразования Галилея в классической механике. Однако, кроме различия, есть и значительное сходство.
Читать дальшеИнтервал:
Закладка:










