Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Такое утверждение противоречит принципу относительности. Все инерциальные системы отсчета совершенно равноправны, и, конечно, нельзя думать, что в одной системе время течет быстрее, чем в другой.

Когда говорят о лоренцовом сокращении времени, всегда имеют в виду только то утверждение, что было приведено выше [76] .

Полную равноправность понятия времени в разных инерциальных системах хорошо поясняет одна иллюстрация.

Представьте две ракеты с радиостанциями на борту. Пусть летчики снабжены физически идентичными часами. Пусть ракеты разлетаются с постоянной относительной скоростью v и каждую секунду по своим часам радиостанция каждой ракеты посылает радиосигналы.

Наблюдатель на ракете № 2, измеряя по своим часам интервалы между моментами приема радиосигналов, посланных ракетой № 1, обнаружит, что они несколько больше одной секунды. А именно:

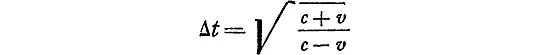
каждый.

Это растягивание времени между двумя последовательными приемами сигналов определяется эффектом Допплера [77] .

Если теперь наблюдатель в ракете № 2 произведет несложный расчет, он заключит, что по его часам n -й сигнал был отправлен в момент времени

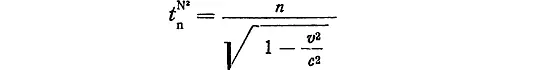
секунд.

(Расчет воспроизводить не будем и поверим, что здесь нет ошибки.)

Но поскольку по часам ракеты № 1 n -й сигнал был послан в момент t n N = n секунд, наблюдатель в ракете № 2 заявит, что часы ракеты № 1 отстают.

Действительно, между отправлением первого и n -го сигналов с ракеты № 1 по часам ракеты № 2 прошло 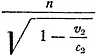секунд, а по часам ракеты № 1 меньше, всего n секунд.

Но ведь вся задача сформулирована совершенно симметрично, и ракета № 1 ничем не лучше ракеты № 2. Поэтому ясно, что в нашем рассуждении можно спокойно переменить номера ракет. И с теми же основаниями наблюдатель в ракете № 1 будет утверждать, что отстают часы ракеты № 2.

Кто же прав?

Оба.

Чтобы это несколько необычное утверждение стало понятнее, надо только уточнить, что подразумевает наблюдатель ракеты № 1, определяя время отправления n-го сигнала с ракеты № 2 по своим часам .

Это время по самому своему смыслу есть не что иное, как показания часов, синхронных с часами ракеты № 1 и находящихся в той точке , где в момент отправления n -го сигнала была ракета № 2.

По сравнению с показаниями этих часов часы ракеты № 2 будут показывать меньшее время — отставать. Точно так же, утверждая, что отстают часы ракеты № 1, наблюдатель в ракете № 2 мысленно «вешает» часы, синхронные со своими, в точку, где находится ракета № 1.

Мы снова приходим к старому выводу. Отстают те часы, которые сравниваются с показаниями нескольких синхронных между собой часов другой инерциальной системы.

В таком виде это заявление выглядит несколько формально, но по смыслу оно совпадает с основным утверждением об измерении промежутка времени между двумя событиями. Интервал времени минимален в той системе отсчета, где события произошли в одной точке [78] .

Однако, честно признаемся, изменение ритма часов воспринимается тяжелее, чем лоренцово сокращение длины. Это вызвано, вероятно, отчасти тем, что вообще труднее воспринять понятие времени, а отчасти «необратимостью» эффекта. Что именно подразумевается под «необратимостью», лучше всего пояснить, вспомнив о длине.

Разгоним стержень относительно какой-либо инерциальной системы до скорости, близкой к скорости света, а затем затормозим его. Предположим, что при малых ускорениях по-прежнему справедливы формулы специальной теории относительности. Тогда наблюдатель, покоящийся в нашей системе, измеряя в процессе движения длину стержня, должен получить примерно такой график.

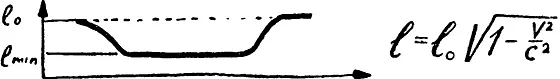
В начальный момент длина стержня равна nl 0, затем с ростом скорости она постепенно уменьшается. Когда скорость достигает максимального значения v и стержень двигается по инерции, длина его остается некоторое время постоянной. Потом по мере торможения она монотонно растет, возвращаясь к прежнему значению l 0. После окончания движения стержень «забывает», что он двигался. Его длина остается неизменной.

Со временем положение иное.

Если «разогнать» часы С (например, поставив в некую фантастическую ракету) и заставить их некоторое время двигаться со скоростью v , а потом затормозить, то после остановки они не будут показывать то время, что часы В , синхронные с А и находящиеся «на остановке».

Часы С отстанут от В . В этом случае обратимой величиной оказывается ритм часов. После путешествия часы С будут идти так же, как до полета (синхронно с А и В ). Но время путешествия, которое они отмерят, будет меньше времени, измеренного по часам А и В . При этом мы снова предположим, что, если часы двигались с не очень большим ускорением, можно с хорошей степенью точности определять измерение их ритма в каждый данный момент, используя формулы специальной теории. То есть:

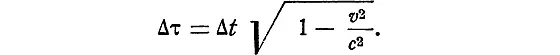
Вообще-то как задача определения длины ускоренно движущегося тела, так и вопрос о ходе времени на этом теле не могут быть решены с помощью специальной теории относительности .

Специальная теория рассматривает только инерциальные системы, и поэтому в наших рассуждениях выводы специальной теории, строго говоря, незаконно распространялись на более общие случаи.

Однако общепринято считать: если ускорения в некоем определенном смысле малы [79] , это можно делать.

Впрочем, некоторые ученые возражают против такого вывода, считая использование специальной теории незаконным. Но мы будем слепо следовать за большинством.

Еще раз повторим: сейчас обсуждается проблема, строго говоря, «не подсудная» специальной теории. Полное решение вопроса может быть получено только в общей теории относительности.