Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

По этому поводу можно высказать совершенно общее утверждение. Заранее ясно, что в теории Эйнштейна как предельный случай должна заключаться классическая механика. Механика Ньютона многократно оправдывалась при проверке на опыте, и никакая разумная новая теория не может просто ее отбросить. От подобных неприятностей классическую механику метод принципов Ньютона страхует навечно.

Как бы ни изменились принципиальные положения, что бы ни оказалось в дальнейшем, но когда скорости тел малы, любая теория должна давать те же или, точнее, почти те же результаты, что и механика Ньютона. Как приближение к истине законы Ньютона останутся навсегда.

Все, что сказано сейчас о механике Ньютона, можно дословно повторить по отношению к специальной теории относительности. Дальнейшее развитие науки может внести любые изменения. Может произойти все что угодно, но хотя бы как приближение к истине теория Эйнштейна останется в науке навсегда.

Вернемся, однако, к конкретному вопросу. Как можно увидеть, что теория Эйнштейна включает в себя механику Ньютона? В этом легко, например, убедиться при анализе любого вывода теории. Ограничимся только одним примером. Когда v / c << 1 можно пренебречь членами ( v / c ) 2и ( v 2/c 2) и формулы преобразования Лоренца переходят в хорошо известные классические формулы преобразования Галилея:

x = x 1 + vt 1;

y = y 1;

z = z 1; t = t 1.

С другой стороны, преобразование Лоренца переходит в преобразование Галилея, если устремить с к бесконечности. Здесь физическое содержание тоже очень прозрачно. Бесконечная скорость распространения сигналов — это гипотеза, как помните, лежит в основе классической физики.

А теперь разрешите совсем маленькую сенсацию.

По существу, наша работа уже почти закончена. Вся специальная теория относительности непосредственно вытекает из двух постулатов, которые мы разобрали в предыдущих главах.

Самое основное изменение, которое вносится в классическую физику, — это изменение понятия времени, или, что то же, изменение понятия одновременности. Сей вопрос также рассмотрен. Мы не касались только одного вывода совершенно принципиального характера — связи между массой и энергией. Но это потом.

Так как математическая часть теории основана целиком на преобразовании Лоренца, которое нами рассмотрено, то все остальное, в том числе сокращение длины и изменение времени, не более чем простые следствия.

Итак, перейдем к рассмотрению частностей с приятным сознанием, что основы уже ясны. Во-первых — закон сложения скоростей.

Постановка вопроса очевидна.

Пусть в инерциальной системе К со скоростью v 1движется некое тело. Пусть далее другое тело движется относительно первого со скоростью v 2. Требуется определить скорость второго тела относительно системы K .

Доставив себе удовольствие строгой и общей формулировкой проблемы, вернемся к железной дороге.

Поезд идет по полотну дороги со скоростью v 1 относительно полотна . (Конечно, его скорость может быть близка к скорости света.) Некто в поезде по не интересующей нас причине стреляет из ружья, и скорость пули — относительно поезда — v 2. Требуется определить скорость пули относительно полотна дороги. (Конечно, и скорость пули v 2тоже может быть близка к скорости света.) Мы ограничимся только тем частным случаем, когда скорости v 1и v 2направлены по одной прямой, но все характерные черты теории относительности великолепно видны и в этом случае.

В классической механике суммарная скорость определялась предельно простым выражением v сум = v 1 ± v 2(знак + в том случае, когда стреляют по ходу поезда, и знак –, когда против хода).

По Эйнштейну, закон для определения суммарной скорости другой:

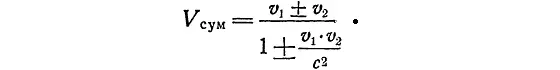
Как видно, если v 1 << c и v 2 << c , формула Эйнштейна переходит в классическую. (В этом случае можно спокойно пренебречь вторым членом знаменателя по сравнению с единицей.) Если же скорости v 1и v 2сравнимы со скоростью света, тогда формула Эйнштейна становится совершенно отличной от классической.

Лучше всего в этом можно убедиться, положив одну из скоростей (например, v 2) равной скорости света. Если помните, мы уже упоминали об этой задаче, обсуждая в XI главе, какова будет относительно полотна дороги скорость светового луча, посланного источником, находящимся на поезде. Легко видеть, что независимо от v 1абсолютная величина суммарной скорости снова равна скорости света.

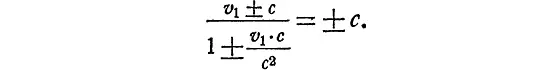
Теперь можно разбить наши рассуждения в XI главе. Как помните, там, защищая баллистическую гипотезу, мы принимали как самоочевидный факт классическую формулу сложения скоростей.

И вот, как оказывается, именно это и неправильно.

Фронт световой волны, идущей из прожектора поезда, распространяется со скоростью с относительно поезда. Но относительно наблюдателя на земле он распространяется не со скоростью ( v поезда + c ), а снова с той же скоростью c .

Для нашего воображения, воспитанного на классической механике, это удивительно. Удивительно, но тем не менее правильно.

Более того, относительная скорость двух фотонов, несущихся навстречу друг другу со скоростью света, снова равна c , а не 2 c , как в классической физике [70] .

В механике Эйнштейна скорость света в вакууме представляет барьер, через который невозможно перебраться.

Как измерять длину движущихся тел, мы уже договорились в III главе. Напомним: «Длина движущегося тела есть расстояние между одновременно отмеченными положениями его начальной и конечной точек».

В классической физике длина движущегося тела, определенная таким образом, совпадала с длиной неподвижного тела, и все было хорошо. Еще и еще раз напомним: