Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Знакомый с силами Кориолиса читатель легко заметит: установив, что какое-то свободное тело покоится, еще нельзя утверждать, что система отсчета инерциальна. Строго говоря, одного свободного тела вообще недостаточно для проверки системы отсчета «на инерциальность». Необходимо исследовать движение трех тел, движущихся не в одной плоскости. Но это уже тонкости.

В реальном опыте Фуко характер «розетки», вырисовываемой маятником, другой, но это связано с несущественными для нас деталями опыта.

Можно только заметить, что если, исследуя понятие инерциальной системы в рамках классической механики, как-то удалось свести концы с концами, использовав понятие тела, достаточно далеко удаленного от всех остальных, то с точки зрения теории относительности такая постановка вопроса совершенно неудовлетворительна. Оказывается, что слова «достаточно далеко» вообще не имеют смысла.

Два тела могут находиться «очень далеко» друг от друга, если измерять расстояние между ними в одной системе отсчета. И «очень близко», если измерять расстояние между ними в другой системе, равномерно и прямолинейно движущейся относительно первой. (Это замечание будет понятно для тех читателей, кто доберется до XIII главы.)

Так что на самом деле положение с понятием инерциальной системы еще хуже, чем может показаться на первый взгляд. Правда, известную определенность в этот вопрос внесли работы Эйнштейна, но мы ничего о них не скажем.

Пользуясь предельно глубокой аналогией, можно сказать: Декарт постулировал нечто вроде мирового сепаратора.

Можно без труда показать, что шар (Земля) притягивает тела так же, как если бы вся его масса была сосредоточена в центре.

«Материальной» здесь означает — состоящей из мельчайших частиц.

Субтильный — тонкий, хрупкий.

Именно кольца Ньютона — первый эффект, в котором проявились периодические свойства света, и именно Ньютон первый это понял.

Два луча на выходе получаются тогда, когда соответствующие кристаллографические оси либо совпадают, либо угол между ними составляет 90°. Поэтому, поворачивая нижний кристалл на полный угол в 360°, мы 4 раза будем наблюдать на выходе 2 луча вместо 4.

Турмалин тоже двояко преломляющий кристалл, но один из лучей в нем полностью поглощается.

Конечно, мы снова отказываемся от разбора этих работ.

Наблюдатель, естественно, отмечает момент t T. Момент t 1можно установить только при помощи расчетов, зная также r 1и C .

Точное значение, как известно, 299 976 км/сек .

Для простоты рассматривается случай, когда звезда находится в плоскости земной орбиты (в плоскости эклиптики).

Несущественная для нас тонкость! Если звезда находится не в плоскости эклиптики, ее видимое движение происходит по эллипсу, подобному земной орбите, как она представляется со звезды.

Между прочим, по годичному параллаксу звезды определяют ее расстояние до Земли. В наши дни параллакс определяют с точностью 0,01″. Это угол, под которым человеческий волос виден с расстояния 1,5 километра!

«Аберрация» дословно означает «отклонение», «заблуждение». Поэтому не приходится удивляться, что термин «аберрация» используют также для обозначения совершенно отличных по своей природе физических явлений, связанных с искажением хода световых лучей. Существует еще «хроматическая аберрация», «сферическая аберрация», «продольная аберрация» и еще несколько аберраций.

Орбитальная скорость Земли была известна — 30 километров в секунду.

Следует напомнить, чтó мы понимаем под неподвижным эфиром. Эфир считается покоящимся в системе неподвижных звезд.

Отношение скорости Земли к скорости света равно 30 км/сек / 3 · 10 5 км/сек = 10 –4. Тангенс такого малого угла с высокой степенью точности равен самому углу (угол измеряется в радианной мере). Поэтому

φ = v / c .

Этот эксперимент проделал, в частности, Эйри (1872 г.). Но если верить Майкельсону («Лекции по оптике»), у Эйри были предшественники, причем эксперимент был сделан, во всяком случае, до опытов Физо (1852 г.). Точную ссылку на работу Майкельсон не дает.

Например, Максвелл подметил, как из опытов Ремера можно «выловить» движение солнечной системы в целом относительно эфира уже «в первом порядке». Подробнее см.: Ландсберг , Оптика.

В первом примере. Порт — источник света. Корабль — приемник. Катера — световые волны. И наконец, море — неувлекаемый эфир.

Во втором. Корабль — источник. Порт — приемник.

Уже упоминалось, что теория неувлекаемого эфира совершенно аналогична теории распространения звуковых волн в атмосфере. Атмосфера — «неувлекаемый звуковый эфир».

Во избежание путаницы надо представлять, что поскольку (как мы увидим дальше) теория неувлекаемого эфира неправильна, неправильно и дальнейшее описание опыта.

Здесь впервые используются приближенные вычисления, на которые, несмотря на их важнейшее значение, мало обращают внимания в школе. Поэтому поясним вывод как приведенной формулы, так и еще одной, неоднократно используемой в дальнейшем.

Если α очень мало, можно утверждать, что

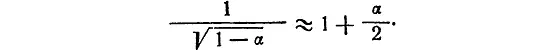
Доказать это очень просто.

Пункт № 1 . Когда α мало, то

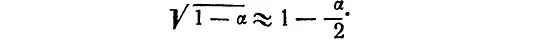
Действительно, возводя обе части приближенного равенства в квадрат, получаем 1 – α ≈ 1 – α + α 2/4.

Правая часть равенства больше левой на α 2/4, но если α << 1, то α 2совсем уже малая величина и ею можно пренебречь (если, например, α = 0,001, α 2 = 0,000001).

Итак, с точностью до членов порядка α 2,

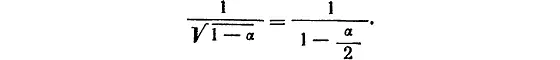
Пункт № 2. Умножим числитель и знаменатель дроби 1/(1 – α/ 2) на 1 + α/ 2. Получим, что

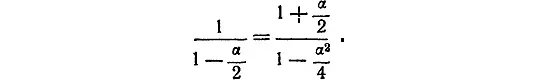
Как и раньше, можно пренебречь членом α 2/4 в знаменателе. Тогда окончательно

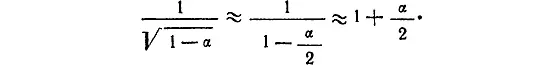
Это равенство справедливо с точностью до членов порядка α 2. Не следует опасаться, конечно, того, что мы пренебрегали членами порядка α 2не один, а два раза. Это не может сколько-нибудь заметно увеличить ошибку.