Петр Путенихин - Правила счета элементов бесконечного множества

"Но вдруг и квадрат можно как-то разбить на части, а потом эти части положить на прямую, чтобы они не задевали друг друга?" [3, с.59].

Алгебраически с учетом равной метрики, как показано выше, это возможно: вытянуть квадрат в линию. Такой способ совмещения, алгебраический сразу же высвечивает противоречивость решения Кантора. К сожалению, автор цитаты не стал развивать эту идею дальше.

Для сравнения двух множеств точек следует попытаться установить однозначное соответствие между этими точками, то есть, показать, что точки обоих этих множеств можно объединить, скажем, в пары (a, b), такие, что каждый элемент, каждая точка a принадлежит линии, а каждый элемент, точка b – квадрату, причем каждый из элементов a и b попал только в одну пару [3, с.59].

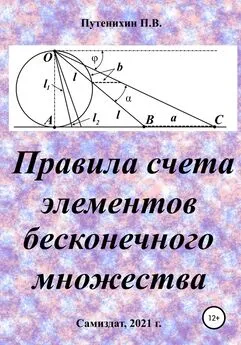
Согласно Кантору два бесконечных множества – точки линии и квадрата – имеют одинаковое количество элементов, если между этими элементами можно установить указанное однозначное соответствие. В математике обычно говорят о мощности множества, подразумевая под нею количество его элементов. Следовательно, отрезок и квадрат, построенный на нем, по Кантору имеют одинаковую мощность. Для доказательства этого он использует следующий метод. В системе координат x0y простроен квадрат ABCD, причем точка A совпала с началом координат, а точка B лежит на оси x. Не всякий способ позволяет установить взаимное однозначное соответствие между точками квадрата и отрезка:

"Проектирование точек квадрата на отрезок АВ здесь не помогает, ведь при проектировании в одну точку отрезка перейдет бесконечное множество точек квадрата (например, в точку А – все точки отрезка DA)" [3, с.77].

Однако такое обоснование нас, разумеется, устроить не может, поскольку это решение верное, но оно все-таки отбрасывается. Координаты каждой точки квадрата можно представить в мнемоническом виде:

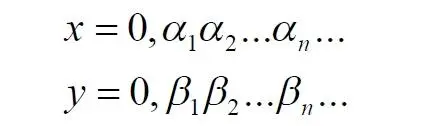
В этих записях каждый символ α, β представляет собой какую-либо цифру из 0…9. То есть, x и y – это просто два дробных числа, меньшие единицы. Здесь следует, кстати, выразить недоумение по поводу отождествления чисел вида 0,50000… и 0,499999....

"…например, 0,500000… и 0,49999999…– это одно и то же число. Для определенности будем пользоваться записью с нулями" [3, с.73].

В частности, вопрос: отождествляются только такие числа? А, например, числа 0,550000… и 0,549999… не отождествляются по такому же принципу? Это правило, собственно говоря, не выдумка. Например, его использует офисная программа MS Excel, правда, с противоположной "определенностью". Там любое целое число в одном из представлений так и записывается: с множеством девяток в конце. Но в нашем случае мы рассматриваем числа в их абсолютном смысле. Поэтому число 0,5000…1 и число 0,5, число 0,4999999… или даже 0,4999…9998 – это совершенно разные числа. Если же вводить указанное правило (округление), то следовало бы и здесь дать веские обоснования, почему такой участи избежали числа 0,549999… или 0,22229999..... Чем они кардинально отличаются? Если же правило распространить и на них, то сразу же образуется счетная бесконечность чисел, отброшенных в результате безосновательного округления.

Итак, после тривиального преобразования координат точки квадрата в мнемоническую запись, с ними производится манипуляция, которая также не имеет веско аргументированного, рационального смысла. Перетасовыванием знаков двух чисел формируется новое число:

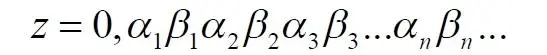
Обратим внимание на следующее интересное замечание и на приведенный далее способ отождествления:

"для простоты мы не берем точки квадрата, лежащие на его сторонах, а берем лишь внутренние точки… Нам надо теперь найти точку Q отрезка АВ, соответствующего точке Т" [3, с.78].

Для "простоты" – это, прямо скажем, – лукавство. Этим упрощением отбрасывается неразрешимое противоречие совпадения линии и стороны квадрата.

Точка T – это точка в квадрате с указанными координатами x и y . Координата точки отрезка выбирается по принципу Q = z . Далее делается ожидаемый вывод: точке T квадрата поставлена в соответствие точка Q отрезка [0, 1]. Следовательно, всем различным точкам квадрата соответствуют разные точки отрезка и тем самым установлено взаимно однозначное соответствие между точками квадрата и точками отрезка. Из этого также делается вывод, что множество точек квадрата имеет такую же мощность (количество), что и множество точек отрезка (их количество).

Такие выводы противоречат не только здравому смыслу, но и логике, поскольку налицо подмена понятий. Сначала обратим внимание на то, что же отождествляется. А отождествляется координата точки отрезка и некоторое комбинационное число , которое вообще-то координатой не является. Действительно, координатой чего мы можем признать сборку – число z ? Какое отношение эта комбинация знаков имеет к координатам x , y точки квадрата? Координаты – это два числа (так сказать, две штуки), а z – это одно число (одна штука). По существу, число z является для координат x , y своеобразным индексом . Иными словами, мы здесь отождествили не две точки, а точку и некий индекс . Но индекс чего? Квадрат – это плоская фигура, следовательно, каждая его часть изначально должна рассматриваться как такая же плоская фигура, фигура с площадью. И мы фактически отождествили не две точки, а точку и площадку , бесконечно малый квадрат. Размеры точек на линии и точек, площадок на квадрате разные, хотя и те и те бесконечно малы.

Конечно, для отождествления это не является противоречием. Мы можем, например, отождествить 10 яблок и 10 уток. Или 200 кресел в кинотеатре и 200 зрителей. Но при этом следует помнить, что равны не они сами по себе, а их количества. В доказательстве Кантора, вроде бы, так и говорится, что равны мощности, равны количества. Однако преподносится это так, что создается впечатление, будто эти сравниваемые множества равны не только по своим количествам, мощности, но и равны буквально – точка на линии тождественно равна точке на квадрате. При таком подходе можно отождествить любые бесконечности, просто отбросив их качество и оставив лишь безликое количество. Все зависит только от искусства отождествителя. Приведём простой пример.

Точки любой линии на плоскости характеризуются двумя координатами. Точно так же и в рассмотренном примере все точки линии имеют две координаты, одна из которых просто равна нулю. Теперь становится ясным, почему мы обратили внимание на замечание " для простоты мы не берем ". На самом деле в таком упрощении преследовалась цель упростить организацию подмены понятий. Ведь если у линии признать наличие имеющейся на самом деле второй координаты, то и для неё пришлось бы также формировать комбинированное число – индекс. Действительно, если вернуть в рассмотрение и стороны квадрата, то одна из них совпадет с отождествляемой линией. В этом случае надо было бы веско обосновать , почему координаты нижней стороны квадрата преобразуются в число z , а линия, полностью совпадающая с этой стороной, по-прежнему описывается одной координатой, хотя у неё однозначно имеется и вторая, нулевая?