Петр Путенихин - Правила счета элементов бесконечного множества

Такая же ситуация будет наблюдаться с индексами и других девяти квадратов. Легко обнаружить, что комбинированные числа каждого квадрата изменяются в диапазонах, соответственно, [0, 0.1), [0.1, 0.2), [0.2, 0.3) и так далее. Таким образом, мы разместили все точки десяти квадратов на одной линии [0, 1]. Получается, что мощность множества, количество точек квадрата имеет меньший порядок, чем мощность множества точек любой линии. В нашем случае – в десять раз. Но мы могли использовать и другое количество квадратов. Тогда и их точки оказались бы во взаимном однозначном соответствии с точками части отрезка. В этом случае соотношение мощностей станет еще больше и даже, по желанию, в любое число раз.

Очевидно, что такой принцип "сколько будет? а сколько надо?", к которому, по сути, сводится метод Кантора, не может служить основой для корректного математического приема. Но в чем же состоит хитрость, изюминка, так сказать, канторовского метода отождествления? По какой загадочной причине происходит такое противоестественное отождествление? В чем его тайный механизм? Ведь мы же четко видим, что каждой точке квадрата можно однозначно привязать каждую точку линии, причем ни одна из точек не останется без своей единственной пары. А тайна, в сущности, предельно проста. Покажем это на еще одном несколько отвлеченном, но подобном примере.

Возьмем для лучшей визуализации квадрат с бесконечным числом точек в количестве… 1000х1000. Конечно, это на самом деле не бесконечность, но число все-таки очень большое – миллион точек, пересчитать которые вручную будет весьма непросто.

Выберем на этом квадрате одну линию, нижнюю грань квадрата. Согласно методу Кантора присвоим какой-то точке квадрата индекс:

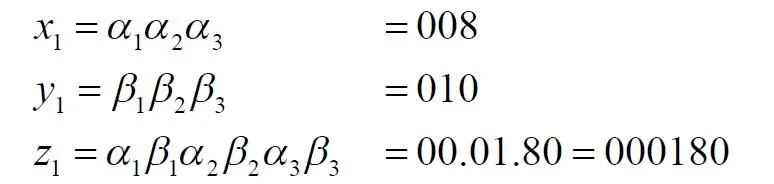
Здесь индекс z сначала представлен с разделительными точками, чтобы было видно, как он образован. Итак, мы получили число z , которое, видимо, точно имеется на отрезке [0, 999]. Правда, настораживает число нулей в этом индексе. Поэтому возьмем для уточнения другую точку на квадрате:

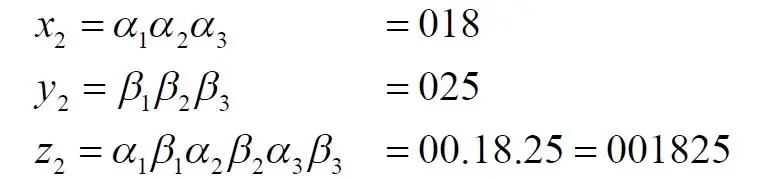
Что-то у нас, как видим, пошло не так. Сразу же можно сделать вывод: на линии [0, 999] такой точки точно нет. В чем же дело? Мы в точности следовали методу Кантора, просто используя отрезок не [0, 1], а более длинный [0, 999]. Принцип тот же, а размеры фигур явно не должны влиять на результат. Иначе получается противоречие: квадрат и линия размером [0, 1] тождественны по мощности, а квадрат и линия [0, 999] имеют уже разные мощности.

Однако именно в этом и состоит хитрость, а по сути подмена понятий в методе Кантора. В нашем случае мы можем попытаться решить проблему такой же дополнительной хитростью. Просто добавим в нашем индексе… запятую. В этом случае подозрительно большое количество нулей сразу превращается в нужное количество:

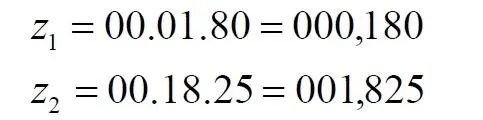
Вот теперь-то каждая из этих точек уже обязана найти своё соответствие на линии. Но возникает другое противоречие. Координаты всех точек квадрата и линии – целые натуральные числа. А здесь мы получили числа дробные, поэтому отождествлять эти индексы с точками линии мы не имеем права. Зато мы обнаруживаем ту самую загадку метода Кантора для отрезка [1, 0]. Фактически индекс формируется методом, схожим с умножением двух чисел. В нашем случае это соответствие должно выглядеть примерно так:

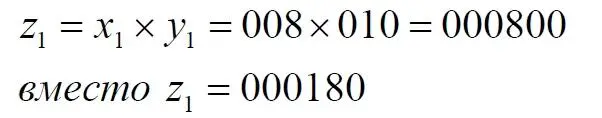
и для второго примера:

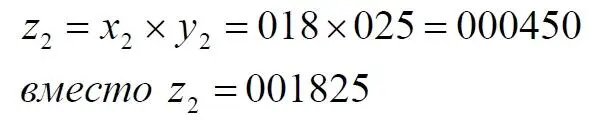
Для сравнения приведем и третий пример:

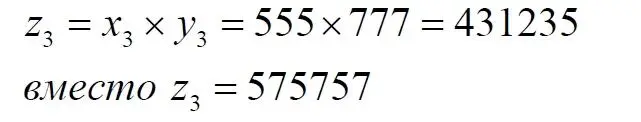
Как видим, оба метода – умножение и перетасовка цифр – дают числа одного и того же порядка с разрядностью площади квадрата (миллион). При этом можно догадаться, что количество разных произведений координат ровно в два раза меньше, чем количество пар сомножителей, поскольку они могут меняться местами. Действительно, пар сомножителей ровно миллион, следовательно, и произведений тоже ровно миллион. Поскольку существуют симметричные пары сомножителей, то их произведения равны. Следовательно, число уникальных произведений равно полумиллиону. Мы полагаем, что произведение разных чисел дают разные результаты.

При перетасовках цифр смешиваемых пар также ровно миллион, следовательно, и результирующих чисел с перетасованными цифрами также будет миллион. Но в этом случае, что довольно странно, среди них не будет одинаковых. Иначе говоря, при умножении пар какие-то значения в ряду из миллиона чисел будут отсутствовать. Это легко обнаружить: при перетасовке пар может быть получено число 999 999, но при умножении пар такое число получено быть не может – максимальное значение произведения равно 998 001. И таких "отсутствующих" произведений пар – ровно полмиллиона.

Несомненная выгода метода Кантора в том, что каждая точка получит свой индивидуальный, уникальный индекс. Однако остаётся проблема: таких индексов заведомо больше, чем элементов в строке, следовательно, и в отождествляемой линии. Искусственно введенная запятая сжимает эти числа до интервала отрезка [0, 999], но множество из них сразу же становятся дробными, то есть, объективно также не могут этому отрезку принадлежать. Увеличение до бесконечности дискретности квадрата и линии сохранит эту тенденцию без отождествления точек квадрата и линии.

А что же с исходным методом Кантора для единичного отрезка? Там, как видим, произведена точно такая же замена умножения двух чисел на перетасовку их цифр, позволившая получить нужное количество индексов. Порядок чисел при умножении и перетасовке по-прежнему один и тот же. Однако индексы или произведения координат имеют больший порядок дискретности , чем каждая из координат, в том числе, и точки отождествляемой линии. И здесь происходит всё та же подмена понятий при подсчете числа элементов в ряду, что и при подсчете числа четных чисел в натуральном ряду. Только здесь каждой точке линии соответствует бесконечное число индексов точек квадрата. И вот почему.

Понятно, что в числах с бесконечным числом знаков разглядеть это весьма непросто, тем более что все они выглядят одинаково, поскольку одинаково начинаются – с нуля и запятой после него. Сравнивая числа – координату линии (q) и координатный индекс z(x, y), например, для q=x=y=0,1 (точное значение), мы находим z=0,11. Дискретность z в этом случае в 10 раз выше, чем дискретность q. То есть, между двумя дискретными значениями q=0,1…0,2 поместится десять подобных индексов. Если q=x=y=0,12345, то z=0,1122334455 и дискретность z уже в 100000 раз больше дискретности q. Следовательно, между точками q=0,11223…0,11224 (это точные значения) поместится 100000 индексов с дискретностью z. Другими словами, беря две координаты с некоторой дискретностью (числом знаков после запятой), мы получаем индекс с удвоенной дискретностью и степенным увеличением их количества. Сравнивая координаты линии и индексы, мы сравниваем фактически не их значения, которые предельно скрыты от нас и не могут быть равны, а их порядковые номера, которые для счетных множеств, разумеется, всегда найдут соответствие.