Петр Путенихин - Правила счета элементов бесконечного множества

Мы, согласно традиции метода, предполагаем, что кому-то удалось пересчитать и перенумеровать все 32 числа в этой таблице. Попробуем доказать, что счётчик всё-таки пропустил, по меньшей мере, одно число. Итак, смотрим на первое число. Его первый разряд равен нулю, поэтому записываем в блокнот единицу: 1nnnn. Остальные четыре цифры нам пока неизвестны. Теперь смотрим на второе число, двигаясь по таблице сверху вниз. Видим, что вторая цифра второго числа равна единице, поэтому записываем в блокнот цифру 0 вторым разрядом нашего числа: 10nnn. Смотрим третье число и видим, что третья цифра равна нулю. Делаем запись в блокнот: 101nn. Таким же образом записываем и четвёртую цифру 1 в блокнот, заметив, что четвёртая цифра четвёртого числа в таблице равна нулю: 1011n. Последнее, пятое число в таблице берём рядом с предыдущим: последнее число в следующей колонке. В результате получаем в блокноте окончательно число 10110. Согласно "блокнотному правилу" наше число отличается от первого первой цифрой, от второго – второй, от третьего – третьей и так далее. Следовательно, мы должны сделать вывод, что счётчик не пронумеровал это число в процессе подсчёта, ведь оно отличается первым разрядом от первого числа… и так далее. Однако… это явно не так. Реально мы просмотрели только 5 (пять) чисел в колонках, хотя общее количество чисел равно 32 – в 6 раз больше. И это, якобы пропущенное число, в этой таблице точно есть. Находится оно в третьей строке в седьмой колонке. Заметим, что порядок просмотра номеров в таблице значения не имеет, просто будут получены разные "пропущенные" номера.

Еще раз отметим, что метод просматривает совсем даже не все числа, а только их количество, равное разрядности числа. Но ведь по условиям рассказа об отелях номеров на этаже – бесконечное количество, то есть, разрядность каждого числа также равна бесконечности. Тем не менее, это ровным счетом ничего не меняет, в этом случае герой рассказа точно так же просмотрит не все числа, а только их часть, и найденное им якобы отсутствующее число обязательно будет присутствовать среди чисел, до которых он просто никогда не дойдёт.

Как говорится, что-то пошло не так. А не так пошло использованное "блокнотное правило". Мы в рассматриваемом общем массиве чисел можем, имеем право просмотреть только 5 (пять!) чисел. Любое следующее число обязало бы нас приписать к "найденному" числу ещё один разряд, но в нашем массиве нет 6-разрядных чисел. Отношение разрядности чисел к их количеству (7) в массиве описывается простым уравнением:

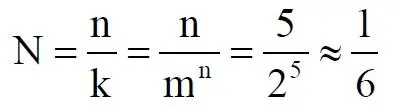
Здесь n – это основание массива: в нашем случае бинарных чисел m = 2. Для десятичных чисел основание m = 10, для шестнадцатиразрядных hex-чисел m = 16. Соответственно, n – это разрядность чисел, в нашем случае n = 5, следовательно, N ~ 1/6. Используя это уравнение, мы можем определить соотношение N и для других, например, для 10-разрядных бинарных чисел:

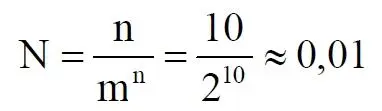
Замечаем, что при увеличении разрядности чисел отношение уменьшается. В пределе, какой рассматривается в задаче об отеле Гильберта, разрядность чисел – номеров комнат в отелях стремится к бесконечности.

Это означает, что при бесконечном количестве комнат счётчик может просмотреть хотя и бесконечное их количество, но в общем количестве комнат это просмотренное количество эквивалентно нулю.

Получается, что доля просмотренных героем рассказа чисел от общего их количества равна нулю, поэтому нет ничего удивительного, что любое найденное им число обязательно будет присутствовать в их полном наборе. Собственно говоря, это тривиальный, очевидный факт: всё бесконечное множество чисел бесконечной разрядности содержит все возможные числа, то есть, это тождественно весь натуральный ряд чисел, поэтому "отсутствующих" чисел в нём быть не может просто по определению.

Такой же результат будет получен, если рассматривать не разрядность, а общее количество чисел.

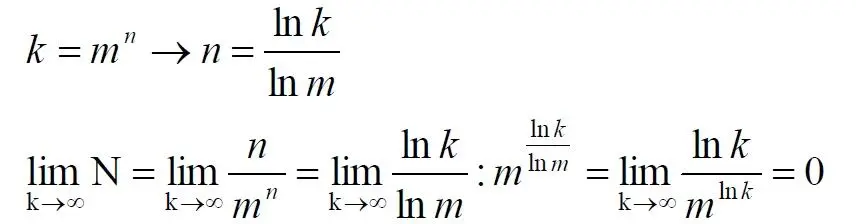
Следовательно, каким бы большим ни был найденный им номер комнаты, якобы не получившей порядкового номера, номера всех комнат используют все без исключения числа от нуля до бесконечности, то есть, содержать все возможные порядковые номера, среди которых обязательно присутствует и "пропущенный" номер.

Таким образом, вывод о несчетности вариантов, номеров комнат является ошибочным. Похоже, что и в управлении космических гостиниц тоже не нашлось грамотного программиста или математика, которые могли бы объяснить директору ошибочность вывода о неполноте списка, и что пари выиграл именно он, директор.

Теперь еще раз обратимся к утверждению о несчетности континуума. Действительные числа являются лишь частью ряда возможных чисел, включающих в себя вещественные, комплексные, кватернионы, гиперкомплексные, поличисла (коммутативно-ассоциативные гиперкомплексные числа), разнообразные многомерные и любые иные виды чисел. Здесь нас не должны интересовать алгебры этих чисел и их свойства. Единственное не обязательное условие – это конечная длина записи числа. То есть, запись числа в виде бесконечного ряда коэффициентов мы пока оставим без внимания, указав, что задача решается так же – предельным переходом.

Все мыслимые числа в общем виде можно записать, например, в следующем виде

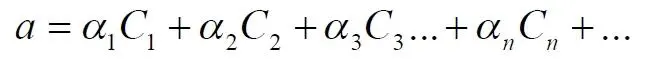
где

α – любое вещественное число;

С – любой индекс, например, мнимая единица i.

Например, число может иметь вид a = 2,71828… –действительное число, или a = 3+2i – комплексное число, или a = 5+2i+3j+8k – кватернион. Правильно организованный способ подсчета этих чисел позволяет показать счетность всего их ряда. Вообще-то, такой результат является простым следствием принятого способа подсчета. На классический вопрос "сколько будет дважды два?" известен шутливый ответ: а сколько надо? По большому счету, всё сводится к спору о том, какой способ подсчета лучше или правильнее. Рассмотрим следующий способ записи всех действительных чисел: запишем после запятой все последовательные натуральные числа "задом наперед", а до запятой – в каждом ряду возрастающие натуральные числа на всём числовом диапазоне. Возникает, например, такой фрагмент последовательности действительных чисел: