Владимир Никонов - Реконструкция обстоятельств ДТП. Введение в современные методы экспертных исследований. Использование краш-тестов

Это правило так же хорошо иллюстрируется с помощью правой руки. Если приложить ладонь к некоторой оси так, чтобы большой палец был направлен вдоль положительного направления оси, и согнуть остальные четыре пальца, то направление их движения покажет положительное направление вращения вокруг этой оси координат, как показано на рис. 1.2.

В дальнейшем использование только правых систем координат позволяет формализовать уравнения, содержащие координаты или их производные, и избежать путаницы со знаками.

В соответствии со стандартом ISO 8855:2011 «Транспорт дорожный. Динамика транспортных средств и курсовая устойчивость. Словарь», ось X – это продольная ось автомобиля, которая всегда направлена вперед. Ось Y – это поперечная ось автомобиля, которая всегда направлена влево от автомобиля.

Тогда, так как система координат правая, то вертикальная ось Z автомобиля направлена вверх. Начало системы координат располагается в центре тяжести автомобиля, чтобы упростить запись уравнений, описывающих его движение. Система координат автомобиля и положительные направления вращения вокруг осей показаны на рис. 1.3.

Для определения координат автомобиля в плоскости достаточно трех параметров: координат центра тяжести автомобиля и угла его ориентации, которым может быть, например, угол между продольной осью автомобиля и осью X неподвижной системы координат.

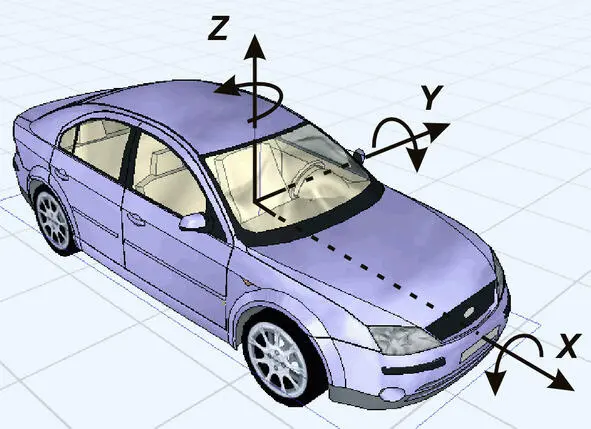
Рис. 1.3. Система координат автомобиля.

Рассмотрим рис. 1.4, на котором показан автомобиль в некоторой неподвижной системе координат XY , связанной, например, с дорогой. В этой системе координат ось X в плоскости чертежа направлена вправо, ось Y – вверх, а ось Z – перпендикулярна плоскости чертежа и направлена к зрителю. Пусть в этой системе координат положение центра тяжести автомобиля определятся точкой O` , которая, в свою очередь, является точкой начала координат X`Y` , связанной с автомобилем. При этом a – угол между осями OX и O`X` .

Как видно из рис. 1.4, в трехмерном пространстве оси координат Z и Z` обоих систем координат, глобальной и локальной соответственно, параллельны друг другу. Отклонение оси Z` от указанного положения в результате удара в автомобиль в большинстве случаев невелико, и этим можно пренебречь.

Поэтому далее для анализа движения автомобиля в плоскости или положения и направления силы удара нам понадобится только двухмерная система координат. Тогда, кроме параметров X C ? Y C и a в глобальной системе координат XY , требуется уметь находить координаты любой произвольной точки автомобиля, известные в локальной системе координат X`Y` .

Пусть некоторая точка M задана координатами (p`,q`) в локальной системе координат X`Y`, связанной с автомобилем. Требуется найти ее координаты (p,q) в глобальной системе координат XY .

Координата p точки M по оси абсцисс есть сумма координаты X C центра тяжести автомобиля (начала локальной системы координат) и разности длин проекции отрезка O`p` на ось абсцисс X и отрезка Cp` .

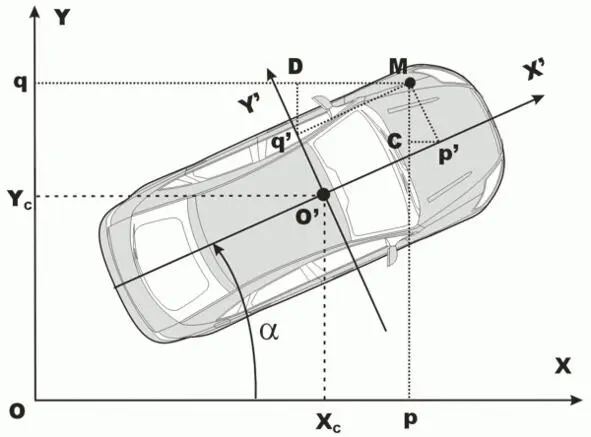
Рис. 1.4. Автомобиль в неподвижной системе координат.

Длина проекции отрезка O`p` на ось абсцисс X есть p`cos (a) . Длина отрезка Cp` есть q`sin (a) .

Тогда координата точки по оси абсцисс есть

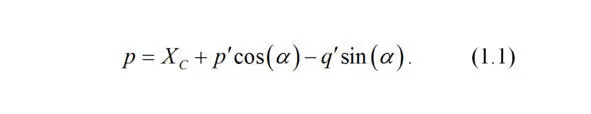
Тогда координата q точки M по оси ординат есть сумма длины проекции отрезка O`q` на ось ординат и длины отрезка q`D , или

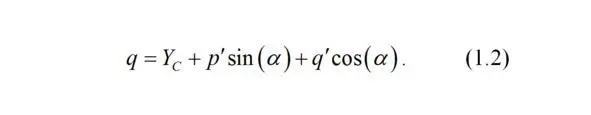
Полученные уравнения важны как для решения задачи движения автомобиля в плоскости, так как позволяют в каждый момент времени определить положение контура автомобиля и его колес в неподвижной системе координат, так и для расчета положения точки приложения силы удара и ее направления.

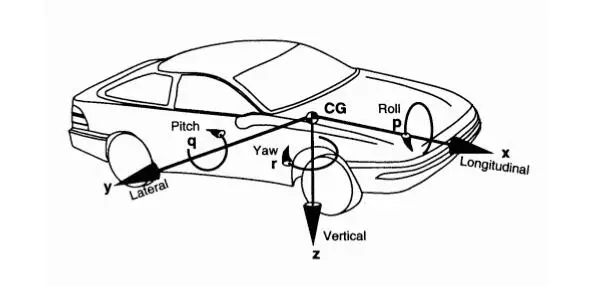
Рис. 1.5. Система координат автомобиля SAE.

В иностранной литературе по реконструкции обстоятельств ДТП для системы координат автомобиля часто используется стандарт Сообщества автомобильных инженеров (англ. Society of Automotive Engineers , SAE ) SAE J670, согласно которому поперечная ось автомобиля Y направлена вправо от автомобиля, а вертикальная ось автомобиля Z направлена вверх, как показано на рис. 1.5.

В этой книге использование системы координат автомобиля SAE оговаривается особо.

1. Стандарт ISO 8855:2011 «Транспорт дорожный. Динамика транспортных средств и курсовая устойчивость. Словарь».

2. Vehicle Dynamics Terminology, SAE J670 JAN2008.

3. Выгодский М. Я. Справочник по высшей математике. – М.: АСТ: Астрель, 2006. 991с.: ил.

Методы реконструкции обстоятельств ДТП базируются в основном на трех законах Ньютона и четырех законах сохранения механики.

Законы Ньютона позволяют записать уравнения движения для любой механической системы, в том числе если известны силовые взаимодействия для составляющих её тел.

Первый закон Ньютона постулирует, что тело находится в покое или движется прямолинейно и равномерно, когда на него не действуют никакие силы (или действуют силы взаимно уравновешенные). Второй закон Ньютона связывает силу, действующую на тело, с его массой и ускорением. Третий закон Ньютона постулирует равенство действия противодействию.

Законы сохранения – фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие совокупность тел, не изменяются с течением времени.

Для реконструкции обстоятельств ДТП важны такие законы сохранения механики, как закон сохранения энергии, закон сохранения количества движения (импульса), закон сохранения момента количества движения (момента импульса), и в ряде случаев закон сохранения массы.

Второй закон Ньютона – дифференциальный закон механического движения, который описывает зависимость ускорения (если ускорение отрицательно, то его называют замедлением) тела от равнодействующей всех приложенных к телу сил F 1 1 Жирным шрифтом или чертой сверху обозначены векторные величины. и массы тела m в виде