Джордан Элленберг - Как не ошибаться. Сила математического мышления

Глубинную структуру задачи с пробоинами в авиационной броне математики обозначают термином «систематическая ошибка выжившего». Такая погрешность часто возникает в самых разных ситуациях [7] Например, истории о том, что дельфины выталкивают тонущих людей на берег. На самом деле дельфины поддерживают тонущего на плаву, подталкивая в произвольных направлениях (что естественно для водных млекопитающих), но только выжившие – те, кого подтолкнули к берегу, – смогли рассказать о встрече с ними. Прим. М. Г. . Зная о существовании систематической ошибки выжившего – как знал о ней Абрахам Вальд, – вы будете готовы к тому, чтобы обнаружить ее, где бы она ни скрывалась.

Возьмем в качестве примера взаимные фонды [8] Взаимный фонд , или фонд взаимных инвестиций (mutual fund), – портфель акций, отобранных и приобретенных профессиональными финансистами на вложения большого числа мелких вкладчиков. Прим. М. Г. . Оценка их эффективности – это именно та область, в которой вам хотелось бы не допустить ни малейшей ошибки. Изменение годового темпа роста стоимости активов фонда на 1 % может составить разницу между ценным инвестиционным активом и убыточным инвестиционным инструментом. На первый взгляд может показаться, что к первому типу инвестиционных активов относятся фонды категории Large Blend (смешанные фонды акций крупных компаний) по версии агентства Моrningstar, показывающие примерно такой же рост, что и индекс S&P 500. За период с 1995 по 2004 год их рост составил 178,4 %, в среднем по целых 10,8 % в год [9] Справедливости ради следует отметить, что сам индекс S&P 500 показал еще более высокий рост – 212,5 % за тот же период. . Похоже, если в то время вы могли бы вложить деньги в те фонды, это принесло бы вам большую прибыль – не так ли?

Так вот, на самом деле все обстоит иначе. Компания Savant Capital в 2006 году провела исследование {9} 9 Amy L. Barrett, Brent R. Brodeski . Survivor Bias and Improper Measurement: How the Mutual Fund Industry Inflates Actively Managed Fund Performance ( http://www.etf.com/docs/sbiasstudy.pdf ). , результаты которого не только проливают свет на эти данные, но и действуют несколько отрезвляюще. Предлагаю подумать, как формируются рейтинги Morningstar. Например, в 2004 году агентство проанализировало темпы роста всех фондов категории Large Blend за прошедшие десять лет.

Но здесь кое-чего не хватает, а именно: фондов, не вошедших в эту категорию . Взаимные фонды не живут вечно. Некоторые из них процветают, тогда как другие прекращают свое существование. К последним, как правило, относятся фонды, не получающие прибыль. Следовательно, оценивать рост стоимости активов взаимных фондов за десятилетний период по данным о фондах, еще существовавших к концу этого периода, – все равно что оценивать эффективность маневров во время воздушного боя, пользуясь методом подсчета количества пробоин в вернувшихся самолетах. Но вдруг мы не обнаружим ни одного самолета, у которого было бы больше одной пробоины? О чем это говорило бы? Конечно, не об умении пилотов мастерски уклоняться от вражеского огня. Скорее всего, это означало бы, что самолеты, получившие два прямых попадания, охваченные огнем, упали на землю.

Результаты исследования компании Savant показывают: если наряду с выжившими фондами включить в расчеты эффективность фондов, прекративших свое существование, рентабельность инвестиций упала бы до 134,5 %, то есть до 8,9 % в год. Показатель гораздо более скромный, не правда ли? Этот вывод подтвердили результаты одного из последних исследований. Журнал Review of Finance провел в 2011 году комплексное исследование, охватившее около пяти тысяч фондов {10} 10 Martin Rohleder, Hendrik Scholz, Marco Wilkens . Survivorship Bias and Mutual Fund Performance: Relevance, Significance, and Methodical Differences // Review of Finance, 2011, vol. 15, no 2, p. 441–474 – см. таблицы. Мы перевели месячную избыточную доходность в годовую избыточную доходность, поэтому цифры в нашем тексте не совпадают с данными, приведенными в статье. . По его результатам было установлено, что избыточная доходность выживших фондов (всего 2641 фонд) оказалась на 20 % выше того же показателя, рассчитанного с учетом данных о фондах, потерпевших неудачу. Возможно, эффект систематической ошибки выжившего удивил инвесторов, но для Абрахама Вальда он, по всей вероятности, не стал бы неожиданностью.

В этот момент мой юный собеседник прервет мой рассказ вполне обоснованным вопросом: ну и где здесь математика? Да, Вальд был математиком, и вне всяких сомнений, его решение проблемы надежности авиационной брони гениально. Но при чем здесь математика? Ни тригонометрических тождеств, ни интегралов, ни неравенств, ни формул.

Прежде всего следует отметить, что математические формулы все-таки были. Я опустил их, рассказывая историю Вальда, поскольку это только пролог. Во введении к книге о размножении человека, рассчитанной на десятилетних ребят, вряд ли стоит во всех подробностях рассказывать, как детки попадают в мамин живот. Нет, мы напишем что-нибудь в таком роде: «В природе все меняется. Зимой деревья сбрасывают листья, весной снова цветут; обычная гусеница прячется в свой кокон и выходит из него, превратившись в прекрасную бабочку. Ты тоже часть природы, поэтому…»

Мы с вами сейчас находимся именно в такой части книги.

Но мы взрослые люди, поэтому давайте на секунду уйдем от расплывчатых формулировок и посмотрим, как выглядит типичная страница реального отчета Вальда {11} 11 Abraham Wald . Method of Estimating Plane Vulnerability Based on Damage of Survivors. Alexandria, VA: Center for Naval Analyses, repr., 1980, July, CRC 432. .

…можно вычислить нижний предел Q i . Мы предполагаем, что разность между значениями q i и q i +1 находится в определенных пределах. Следовательно, можно вычислить верхний и нижний пределы Q i .

Предположим:

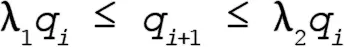
где λ 1 < λ 2 < 1, таковы, что выполнено:

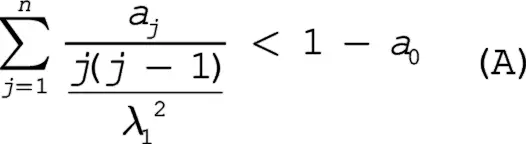
Точное решение слишком громоздко, но можно рассчитать приближенные значения верхнего и нижнего пределов Q i для i < n посредством следующей процедуры. В расчетах используется такой набор гипотетических данных:

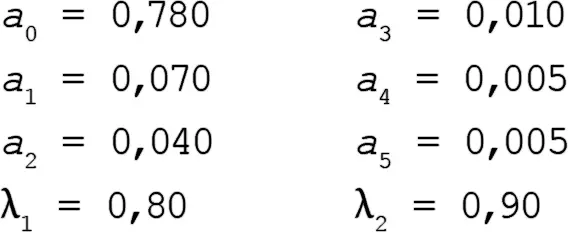
Условие А удовлетворено, поскольку подстановка дает нам значение

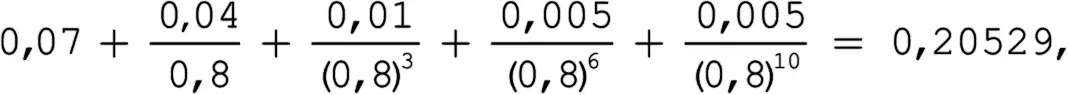
что меньше, чем

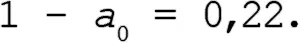
НИЖНИЙ ПРЕДЕЛ Q I