Анджей Ясинский - Ник. Чародей

С математической точки зрения, в таком определении существует некоторое неудобство, связанное с тем, что координаты физических событий имеют разные единицы измерения по разным осям (метры и секунды). С другой стороны, данное неудобство легко устраняется путем умножения времени на размерную константу.

Чтобы определить такую константу, обратимся к понятию интервала в теории относительности:

S 2= x 2+ y 2+z 2— c 2t 2(1.3).

В данном выражении мы видим несимметричность относительно времени. И избавиться от такой несимметричности можно, только введя перед временем комплексный множитель. Заменим время в данном выражении на комплексную величину:

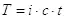(1.4),

где 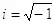(мнимая единица),

с — коэффициент имеющий размерность скорости (скорость света),

t — время,

и назовем данную величину метрическим временем. В итоге выражение интервала в новой системе измерения примет следующий вид:

S 2= x 2+ y 2+z 2+Т 2 (1.5)

Замена обычного времени на метрическое является всего лишь математическим приемом и приведет к изменению вида известных физических законов. Основной проблемой при рассмотрении полученного пространства будет наличие комплексного множителя у таких привычных понятий, как время и скорость, что может затруднить интерпретацию получаемых результатов, но с математической точки зрения, мы всегда можем сделать обратное преобразование к привычному времени и перевести полученные результаты в пространство Минковского.

Исходя из этих соображений, при рассмотрении физических законов перейдем от привычного пространства Минковского к новому четырехмерному пространству, первые три координаты которого совпадают с привычным трехмерным пространством, а четвертая координата является метрическим временем, т.е. временем, имеющим размерность расстояния (Т). Для удобства в дальнейшем будем называть эту систему координат ТR-пространством.

Очень легко определить основные соотношения в ТR-пространстве, для чего достаточно во всех формулах поделить время на комплексный множитель ic. Для новых величин будем использовать индекс i, а координаты будем писать большими буквами X, Y, Z. Кроме того, величины скорости, импульса и энергии будем также отмечать индексом i.

Итак, мы определили пространство событий, которое поможет ввести понятие информации в физическое рассмотрение. Теперь осталось понять, как определяется вероятность различных событий в нашем пространстве. С точки зрения классической механики, понятие вероятности не имеет физического смысла, так как движение всех материальных тел предопределено законами взаимодействия и вероятность любого события либо равна единице, либо нулю. Такая ситуация возникла из-за того, что классическая механика строилась на основе рассмотрения материальных точек нулевого размера, у которых возможно определение координат с любой точностью. Причем оба этих допущения являются некоторой идеализацией реальной физической картины. Логично будет предположить, что отказ от таких предпосылок должен приблизить физическую теорию к реальности, хотя и существует риск значительного усложнения физической картины.

Исходя из вышеизложенных соображений, заменим понятие материальной точки на определение физического объекта, который определим как произвольную сущность, ограниченную в четырехмерном пространстве (имеющую конечные размеры по всем четырем осям, включая ось времени).

Данное определение выбрано как наиболее общее и под него попадают все известные материальные объекты.

Теперь приступим к рассмотрению простейшего объекта, состоящего из двух взаимодействующих частиц в нашем новом TR-пространстве.

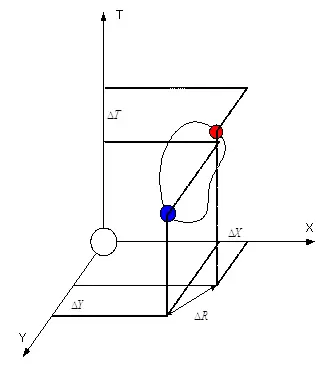
Рисунок 1.

На рисунке 1 изображена четырехмерная система отсчета, привязанная к объекту, находящемуся в начале координат. В данной системе представлен второй объект, состоящий из двух произвольно взаимодействующих частиц. Сплошной линией показана мировая линия взаимодействующих частиц (четырехмерная траектория). Для удобства восприятия не отображена третья пространственная координата, но подразумевается, что движение происходит по всем направлениям. Движение взаимодействующих частиц происходит внутри объема, ограниченного четырехмерной поверхностью, и данный объем имеет проекции на все оси системы отсчета 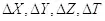. Ключевым моментом в данной картинке является наличие размера объекта вдоль временной оси. В классической физике такой момент не подразумевался, и поэтому данный факт вызывает трудности восприятия. В дальнейшем мы покажем, что наличие размеров вдоль временной оси является обязательным для всех типов объектов, а пока, забегая вперед, только скажем, что данный размер равен периоду колебаний взаимодействующих частиц в пространстве.

Вероятность нахождения объекта в любой точке пространства будет равна отношению объема объекта к объему всего пространства.

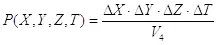(1.6),

где 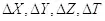— размеры объекта,

— полный четырехмерный объем рассматриваемого пространства.

В качестве полного объема пространства пока можно использовать любое очень большое число, например, объем видимой вселенной. В дальнейшем мы увидим, что при дифференцировании данный параметр исчезает и от него ничего не зависит.

Теперь можно использовать определение информации 1.2, чтобы определить количество информации о местоположении объекта, которое будет выражаться через логарифм вероятности нахождения объекта в некоторой точке пространства.

(1.7)

Полученное выражение имеет одно значение для всех точек пространства, которое зависит только от размеров объекта. При этом мы определили, что наш объект состоит из двух взаимодействующих частиц, и размерами объекта будет проекции расстояния между частицами на соответствующие оси. И в результате получается, что данная функция зависит от взаимного местоположения взаимодействующих частиц в различные моменты времени. Чтобы изучить поведение данной функции, найдем ее производную по времени:

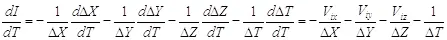(1.8),