Анджей Ясинский - Ник. Чародей

где 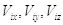— скорость изменения расстояния между частицами вдоль соответствующих осей. У данных скоростей мы используем индексы i, которые показывают, что производная берется по комплексному времени, а чтобы перейти к обычным скоростям, нужно использовать комплексный коэффициент ic.

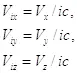(1.9)

Полученная нами функция 1.8 выражает скорость изменения информации о местоположении объекта, которая зависит от движения взаимодействующих частиц, составляющих объект.

В философском смысле сущность информации является базовой и достаточной для описания любых процессов. Если распространить такой взгляд на введенную нами физическую информацию, то можно предположить, что данная функция будет описывать поведение системы на основе данных о координатах и скоростях частиц, составляющих систему. Подобная функция используется в классической механике, и она называется лагранжианом системы. Исходя из данных соображений, проверим функцию 1.8 на совместимость с уравнением Лагранжа:

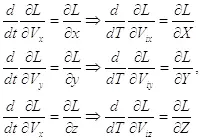(1.10)

В данных уравнениях мы произвели переход к комплексному времени, в результате чего скорости в них также стали комплексными, что отмечено добавлением индекса i. Следует отметить, что уравнения Лагранжа полностью сохранили свой вид при таком преобразовании.

Вычислим частные производные по скоростям и продифференцируем их по времени.

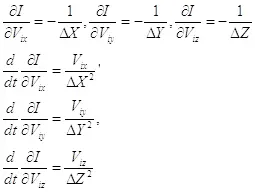(1.11)

Частные производные по координатам вычисляются следующим образом:

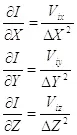(1.12)

В результате получаем полное совпадение выражений 1.11 и 1.12, которое говорит о том, что скорость изменения информации можно использовать в качестве лагранжиана системы двух взаимодействующих частиц.

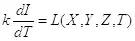(1.13),

где k— размерный коэффициент, определяющий единицы измерения,

L — функция Лагранжа.

В свою очередь лагранжиан связан с определением функционала действия, на основе которого построена вся современная механика. При этом принцип наименьшего действия выражается следующей формулой:

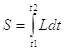(1.14).

Подставив в него скорость изменения информации, получим:

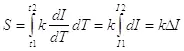(1.15).

Данная формула определяет, что действие между двумя событиями совпадает с разностью информации между данными событиями.Получается, что введенное нами понятие физической информации совпадает с понятием действия, на основе которого сформулирован базовый принцип физики — принцип наименьшего действия.

Таким образом, мы можем сформулировать принцип наименьшего действия через функцию информации.

Каждая механическая система характеризуется потоками информации, скорость изменения информации является функцией координат объектов, составляющих систему, а также их производных по времени.

Движение системы между двумя точками происходит по той траектории, на которой изменение информации будет минимальным.

Подведем промежуточный итог наших рассуждений. Для того чтобы ввести понятие информации в физическую картину, нам пришлось изменить две базовых предпосылки классической механики. Во-первых, мы отказались от рассмотрения материальных точек из-за отсутствия у них пространственных размеров и перешли к рассмотрению объектов, ограниченных в пространстве. Кроме того, для получения изотропности четырехмерного пространства мы переопределили временную координату, умножив ее на размерную комплексную константу. На примере системы двух взаимодействующих частиц мы применили определение собственной информации из математической теории информации и получили функцию, зависящую от размеров системы. Рассмотрев производную данной функции, мы увидели, что она является лагранжианом системы и полностью описывает ее состояние. Кроме того, информация совпадает с функционалом действия и через нее красиво выражается базовый принцип механики — принцип наименьшего действия. Такие результаты позволяют с уверенностью утверждать, что полученная нами функция информации является базовой в физической картине и ее удобно использовать для описания широкого спектра физических явлений.

Имея функцию Лагранжа для системы, мы можем определить энергию, импульс и законы движения. Так, например, частные производные лагранжиана по компонентам скорости будут являться соответствующими компонентами импульса:

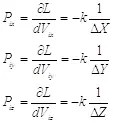(2.1)

Здесь также нужно отметить, что данные импульсы являются комплексными, так как производные берутся по комплексным скоростям. Если брать производные лагранжиана по обычным скоростям, то добавится множитель ic :

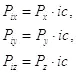
Энергию системы можно получить из лагранжиана, используя следующее выражение:

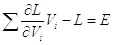(2.2)

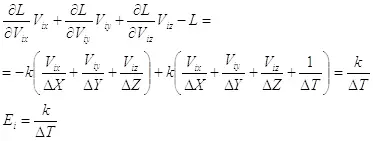(2.3)

Теперь запишем отдельно выражения для компонент импульса и энергии в реальном времени:

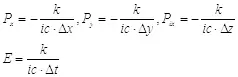(2.4)

Сразу бросается в глаза, что полученное выражение для энергии совпадает с формулой Планка 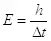, если определить коэффициент k следующим образом:

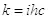(2.6).

И тогда в реальном пространстве получатся следующие выражения:

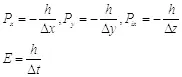(2.7)

Переменная k играет роль постоянной Планка и определяет единицы измерения энергии и импульса, поэтому обозначим ее буквой 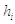, использовав индекс i по аналогии с другими величинами. Кроме того, переопределим введенную нами функцию физической информации, умножив ее на данную константу, и также добавим к ней индекс i: