Anatoly Kondratenko - Probabilistic Theory of Stock Exchanges

Further, similarly to classical mechanics, we can consider prices and quantities of market agents as trajectories of market agents in two-dimensional economic space using the coordinate system [P, Q] as shown in Fig. 1.5. Let us clarify that time t in this parametric representation of functions S&D is an implicit parameter. Generally, this parametric representation gives nothing new compared to Figs. 1.3 and 1.4. Nevertheless, there is one interesting nuance here – the similarity of this diagram with the traditional picture in the neoclassical S&D model, namely the Marshall cross. We will touch on this issue a little later, but for now let's look at some of the features in Fig. 1.5. First, as the arrows show, the buyer and the seller move toward each other in terms of price: the seller lowers it, and the buyer, on the contrary, raises it. Thus the figure reflects normal market negotiation processes. Second, usually during negotiations, quantity quotations are reduced by both agents, i.e. both the buyer and the seller.

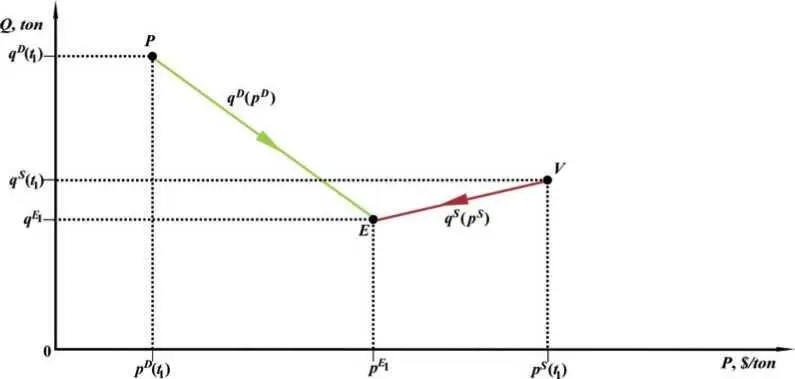
Fig. 1.5. Dynamics of the classical two-agent market economy in the two-dimensional economic space of price-quantity in the first time interval [ t 1,t 1 E ].

Clearly, all agents want to buy or sell less goods at a compromise market price than at the desired prices they stated at the beginning of the trade. These factors together determine that the slope of the demand curve q D(p D) is negative and the slope of the supply curve q S(p S) is positive, just as the S&D functions in the neoclassical model «should» be. But this visual similarity is incomplete, because the economic meaning of these pictures in the two theories differs significantly: in the classical model it is a description of the actual process of negotiations in order to reach a deal, and in the neoclassical model it is a description of strategies of behavior of agents in the market in terms of neoclassical supply and demand curves, q D(p D) and q S(p S). We emphasize that while in neoclassics these curves, by definition, represent as it were the actual functions of supply and demand, in classics these curves are simply a graphical representation of the price and quantitative time trajectories in the form of one trajectory in the course of trading. Thus, the classic economic theory does not assume the existence of any definite dependence of the agents’ quantitative quotations on price quotations, i.e. the existence of any definite functions q D(p D) and q S(p S).

In conclusion, we would like to emphasize that, as we have seen, if agents insist on their initial offers and show no willingness to bargain and compromise, the volume of bargaining will be zero. It is the willingness of the buyer and seller to modify their initial offers that leads to bargains. Thus, we can argue that market agents should initially include into their strategies a certain possible range of prices and quantities for their quotations. From this point, only one important step remains to build a better probabilistic model.

In order to achieve greater transparency of the presentation, we will also reserve ourselves in this section to describing the details of probabilistic theory on the example of the two-agent model of the grain market.

We have come to the most intriguing point in the presentation of probabilistic economics, namely, we will now include the sixth principle – uncertainty and probability – to the theory. We will proceed as follows: first, for the analogy with theoretical physics, or more precisely, with the procedure of transition from classical mechanics to quantum mechanics to be clearly visible, and, second, we will try not to lose key aspects of describing the economic character, i.e. meaningful and rational behavior of agents in the market. The latter concerns, first of all, the process of agents' decision-making about the strategy of behavior in the market as well as the method of mathematical representation of market actions implementing these agents’ decisions. Obviously, taking into account the principle of uncertainty and probability should in one way or another lead us from a point strategy of agents to some continuous strategy. Mathematically we will make this transition in exactly the same way as in theoretical physics we make the transition from temporal trajectories of particles to probability distributions of particles in space. Namely, let us move from a description of economic dynamics in classical economic theory in terms of temporal price and quantity agent trajectories, p D ( t ), q D ( t ), etc., to a description of dynamics in probabilistics using continuous agent distributions of price and quantity probabilities D ( p, q) и S ( p, q ), which we will call probabilistic agent functions S&D. For certainty, let us note that these distributions themselves depend on trajectories, p D ( t ), q D ( t ), etc., so they are themselves functions implicitly dependent on time. In order not to «obfuscate» the formulas by specifying this time dependence everywhere, we will often omit the time variable t in the formulas.

Let us briefly elaborate again on the rationale for this approach to physical-economic modeling. Market agents, forced to constantly work on the market in a continuously changing situation, are aware that the prices and quantities declared by them in the point strategy may not suit the counterparty at a given time. Based on previous experience in the market, they are well aware that they cannot know exactly how prices and quantities will develop in the market even in the near future. They are already used to operating in a market with great uncertainty, entailing high risks and the resulting potential costs. As a result, they realize that in the market they should always consider all their decisions and actions as possible with a certain degree of probability. This probabilistic aspect of the process of market decision-making is of great importance for understanding the behavior of agents in the market and the market as a whole [Mises, 2005; Gilboa et al., 2008]. Market agents think and act as homo oscillans . That is why they are forced to enter the real market not with discrete strategies, but with continuous strategies which can be represented by continuous probability distributions with certain widths correlated with the amount of uncertainty in the market situation in a given period of time.

As already noted, the description of continuous strategies requires the use of two-dimensional functions S&D, D ( p, q ), and S ( p, q ). Of course, it is rather tedious to calculate and analyze two-dimensional functions representing three-dimensional surfaces already in the case of a one-commodity market. For this reason, we will take one more step in simplifying our models, which will make it possible to perform economic calculations of real multi-agent markets and to analyze the results obtained by our method at the highest scientific level. Thus, we a priori assume that we can factorize the agent functions S&D with a sufficient degree of accuracy, i.e. we can approximate their representation as a product of one-dimensional functions as follows:

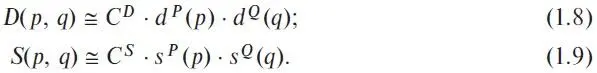
This type of factorization and the corresponding approximation, in which the price and quantitative variables are separated, will be called PQ -factorization and PQ -approximation, respectively. Here d P(p) and s P (p) are one-dimensional price functions, d Q(q) and s Q(q) are one-dimensional quantity functions of S&D normalized by definition to 1:

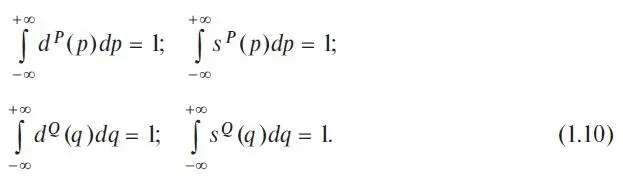
C D and C S are simply normalization factors. They are derived from the condition of such a natural normalization selection of the agent functions S&D:

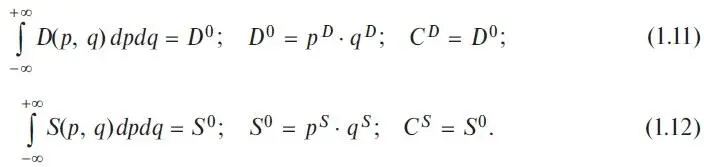
Here D 0and S 0are obviously total demand and complete supply of the buyer and seller, respectively. Below we will also omit the word «total» for the sake of brevity. It is easy to show that the agent S&D-functions, D(p, q) and S(p, q) , normalized in this way, are dimensionless functions. It is also obvious that in the point or discrete strategy described above, one-dimensional functions are represented by the so-called Dirac delta functions as follows:

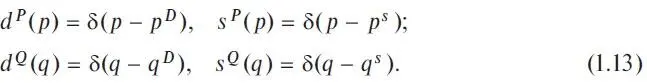
Keep in mind, that the special Dirac function by definition is zero everywhere except at the zero point, where it is equal to infinity, and its integral from minus infinity to plus infinity is 1. By the way, these functions can be applied to describe the probability functions of monopolist and monopsonist supply and demand in real markets.

Accounting for uncertainty in agents' strategies should obviously lead to «blurring» of these functions and turning them into continuous dome-shaped functions with maxima at the points p D, p S, q D и q S and agent widths Г DP, Г SP, Г SQ and Г DQ respectively. It seems reasonable, both from the economic and technical point of view, in the first approximation to use normal, or, simply, Gaussians distributions [Kondratenko, 2015]. Then the demand function has the following form in this approximation:

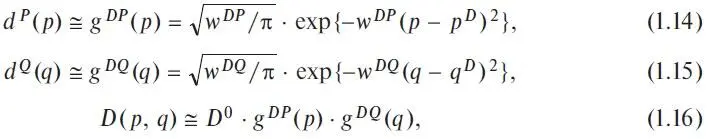
where the parameters w DPand w DQ (agent frequency parameters below) are related to the agent widths as follows:

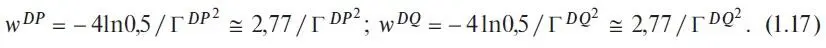
Formulas for demand have a similar structure naturally:

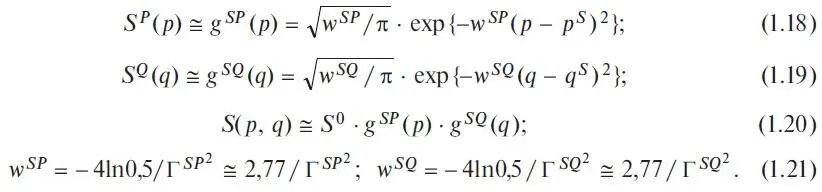
To avoid misunderstandings, note that formulas (1.17) and (1.21) express the relationship known for Gaussians between their agent frequency parameters and the widths, more precisely, the widths of Gaussians at half-height. The numerical values of these widths are set or selected explicitly or implicitly by the agents themselves, just as prices and quantities are set by them. But, very importantly, unlike price and quantity quotations, the «quotations» of widths are not explicitly exhibited either in negotiations or in organized markets. The values of these widths may not even be accurately realized by the agents themselves; in this respect, agents may act purely intuitively, depending on the market situation.

Summing up the intermediate results, we can briefly say that in this version of the theory the buyer's probabilistic demand function is described by four parameters, the price p D , the quantity q D and two widths Г DР and Г DР . The same statement is of course true for the seller's probabilistic supply function. It is these eight parameters that take into account all of the relevant market information that the buyer and seller use before they put up quotations at any given time in the process of trading in the market. And let us emphasize for clarity that usually both buyers and sellers declare or announce publicly and unambiguously only their price and quantity quotations, leaving the information about their widths "behind the scenes".