Ричард Фейнман - 1. Современная наука о природе, законы механики

Точно таким же образом можно определить, что произойдет, когда сталкиваются два одинаковых тела, каждое из которых движется с произвольной скоростью.

Пусть одно тело летит со скоростью v 1 , а другое — со ско­ростью v 2в том же направлении (v 1>v 2 ). Какова будет их ско­рость после соударения? Давайте снова сядем в машину и по­едем, скажем, со скоростью v 2 . Тогда одно из тел будет казаться нам стоящим на месте, а второе — налетающим на него со ско­ростью v 1- v 2 . Эта ситуация уже знакома нам, и мы знаем, что после соударения скорость нового тела по отношению к машине будет равна 1/ 2 (v 1 - v 2 ). Что же касается действитель­ной скорости относительно земли, то ее можно найти, прибавив скорость автомобиля: v = 1/ 2(v 1-v 2)+v 2или 1/ 2(v 1+v 2) (фиг. 10.5).

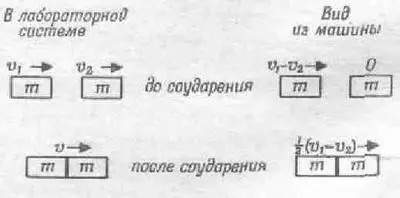
Фиг. 10.5. Другой случай неуп­ругого соударения равных масс.

Обратите внимание, что снова

mv 1+ mv 2=m· 1/ 2(v 1+v 2). (10.6)

Таким образом, принцип относительности Галилея помогает нам разобраться в любом соударении равных масс. До сих пор мы рассматривали движение в одном измерении, однако на основе его становится ясным многое из того, что будет проис­ходить в более сложных случаях соударения: нужно только пустить автомобиль не вдоль направления движения тел, а под каким-то углом. Принцип остается тем же самым, хотя детали несколько усложняются.

Чтобы экспериментально проверить, действительно ли тело, летящее со скоростью v после столкновения с покоящимся телом той же массы, образует новое тело, летящее со скоростью v/2, проделаем на нашей замечательной установке следующий опыт. Поместим в желоб три тела с одинаковыми массами, два из которых соединены цилиндром со взрывателем, а третье на­ходится вблизи одного из них, хотя и несколько отделено от него. Оно снабжено клейким амортизатором, так что прилипает к тому телу, которое ударяет его. В первое мгновение после взрыва мы имеем два объекта с массами m , движущимися со скоростью v каждое. В последующее мгновение одно из тел сталкивается с третьим и образует новое тело с массой 2т, которое, как мы полагаем, должно двигаться со скоростью v/2. Но как проверить, что скорость его действительно v/2? Для этого мы вначале установим тела таким образом, чтобы расстояния до концов желоба относились как 2:1, так что первое тело, которое продолжает двигаться со скоростью v, должно пролететь за тот же промежуток времени вдвое большее расстояние, чем скрепившиеся два других тела (с учетом, ко­нечно, того малого расстояния А, которое второе тело прошло до столкновения с третьим). Если мы правы, то массы m и 2mдолжны достичь концов желоба одновременно; так оно и про­исходит на самом деле (фиг. 10.6).

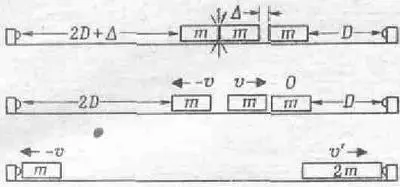
Фиг. 10.6. Экспериментальная проверка того факта, что масса т, ударяя со скоростью v массу m, образует тело с массой 2 m и скоростью v/2.

Следующая проблема, которую мы должны решить: что получится, если тела имеют разные массы. Давайте возьмем массы m и 2mи устроим между ними взрыв. Что произойдет тогда? С какой скоростью полетит масса 2т, если масса mлетит со скоростью v? Фактически нам нужно повторить только что проделанный эксперимент, но с нулевым зазором между вторым и третьим телом. Разумеется, что при этом мы получим тот же результат — скорости тел с массами m и 2mдолжны быть соответственно равны - v и v/2. Итак, при разлете тел с массами mи 2mполучается тот же результат, что и при симметричном разлете двух тел с массами mс последующим неупругим соударением одного из этих тел с третьим, масса которого тоже равна m.Более того, отразившись от концов, каждое из этих тел будет лететь с почти той же скоростью, но, конечно, в об­ратном направлении, и после неупругого соударения они оста­навливаются.

Перейдем теперь к следующему вопросу. Что произойдет, если тело с массой mи скоростью v столкнется с покоящимся телом с массой 2m? Воспользовавшись принципом относитель­ности Галилея, можно легко ответить на этот вопрос. Попросту говоря, нам нужно опять садиться в машину, идущую со скоростью - v/2 (фиг. 10.7), и наблюдать за только что описанным процессом.

Фиг. 10.7. Неупругое соударение между телами с массами m и 2m.

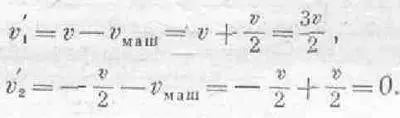
Скорости, которые мы при этом увидим, будут равны

После соударения масса 3m покажется нам движущейся со скоростью v/2. Таким образом, мы получили, что отношение скоростей до и после соударения равно 3:1, т. е. образовав­шееся тело с массой 3mбудет двигаться в три раза медленней; И в этом случае снова выполняется общее правило: сумма произведений массы на скорость остается той же как до, так и после соударения: то + 0 равно 3m · v/3. Вы видите, как по­степенно шаг за шагом устанавливается закон сохранения им­пульса.

Итак, мы рассмотрели столкновение одного тела с двумя. Используя те же рассуждения, можно предсказать результаты столкновения одного тела с тремя телами, двух тел с тремя те­лами и т. д. На фиг. 10.8 как раз показан случай разлета масс 2 mи 3m из состояния покоя.

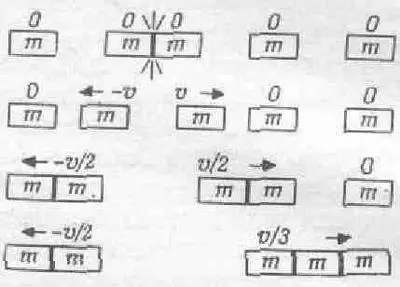
Фиг. 10.8. Разлет тел с массами 2m и 3m.

В каждом из этих случаев выполняется одно и то же правило: масса первого тела, умноженная на его скорость, плюс масса второго тела, умноженная на его скорость, равны произведению полной массы на скорость ее движения. Все это — примеры сохранения импульса. Итак, начав с простого случая симмет­ричных равных масс, мы установили закон сохранения для более сложных случаев. В сущности это можно сделать для лю­бого рационального отношения масс, а поскольку любое число может быть со сколь угодно большой точностью заменено ра­циональным, то закон сохранения импульса справедлив для любых масс.

§ 4. Импульс и энергия

Во всех предыдущих примерах мы рассматривали только случаи, когда два тела сталкиваются и слипаются или с самого начала были скреплены вместе, а потом разделяются взрывом. Однако существует множество примеров соударений, в которых тела не сцепляются, как, например, столкновение двух тел равной массы и одинаковой скорости, которые затем разлетаются в разные стороны. На какой-то краткий миг они соприкасаются и сжимаются. В момент наибольшего сжатия они останавли­ваются и их кинетическая энергия полностью переходит в энергию упругого сжатия (они как две сжатые пружины). Эта энергия определяется из кинетической энергии, которой обладали тела до столкновения и которая равна нулю в момент их остановки. Однако кинетическая энергия теряется только на одно мгновение. Сжатое состояние, в котором находятся наши тела,— это все равно что заряд в предыдущих примерах, который при взрыве выделяет энергию. В следующее мгновение про­исходит нечто подобное взрыву — тела разжимаются, оттал­киваются друг от друга и разлетаются в стороны. Эта часть процесса вам тоже хорошо знакома: тела полетят в разные стороны с одинаковыми скоростями. Однако скорости отдачи, вообще говоря, будут меньше тех начальных скоростей, при которых они столкнулись, ибо для взрыва используется не вся энергия, а только какая-то ее часть, но это уже зависит от свойств материала, из которого сделаны тела. Если это мягкий материал, то кинетическая энергия почти не выделяется, но если это что-то более упругое, то тела более охотно отскакивают друг от друга. Неиспользованный остаток энергии превращается в тепло и вибрацию, тела нагреваются и дрожат; впрочем, энергия вибрации тоже вскоре превращается в тепло. В прин­ципе можно сделать тела из столь упругого материала, что на тепло и вибрацию не будет расходоваться никакой энергии, а скорости разлета в этом случае будут практически равны на­чальным. Такое соударение мы называем упругим.