Нихиль Будума - Основы глубокого обучения
- Название:Основы глубокого обучения
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2020
- Город:Москва
- ISBN:9785001464723
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Нихиль Будума - Основы глубокого обучения краткое содержание
Основы глубокого обучения - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Если рассмотреть NTM в свете беседы о полноте РНС по Тьюрингу, окажется, что дополнение РНС внешней памятью для кратковременного хранения позволяет вырезать из поля поиска существенный сегмент. Ведь теперь не нужно работать с РНС, которые способны и манипулировать информацией, и хранить ее: достаточно найти те, которые могут обрабатывать информацию с внешнего носителя. Такое сужение поля поиска помогает нам частично раскрыть потенциал РНС, до которого ранее было тяжело добраться. Это очевидно по разнообразию задач, которым может научиться NTM: от копирования последовательностей входных данных до эмулирования н-граммных моделей и сортировки данных по приоритетам. К концу главы мы увидим, как расширенная NTM может научиться выполнять задачи на понимание прочитанного, вроде рассмотренной выше, методом градиентного поиска!
Доступ к памяти на основе внимания
Чтобы обучать NTM по методу градиентного поиска, нужно убедиться, что вся архитектура дифференцируема: можно вычислить градиент исходящих потерь по отношению к параметрам модели, обрабатывающим входные данные. Это свойство называется сквозной дифференцируемостью — от входа к выходу. Если мы попробуем получить доступ к памяти NTM так, как цифровые компьютеры обращаются к RAM, через дискретные значения адресов, мы получим разрывность в градиентах вывода и не сможем больше обучать модель градиентным методом. Нам нужен способ постоянного доступа к памяти и возможность «сосредоточиться» на конкретной ее ячейке. И такой постоянной концентрации можно достичь благодаря методам внимания!
Вместо дискретного адреса в памяти мы даем каждой головке возможность создать нормализованный функцией мягкого максимума вектор внимания того же размера, что и число ячеек памяти. Так мы получим доступ ко всем ячейкам памяти одновременно в размытом виде. Каждое значение вектора будет показывать, насколько мы собираемся концентрироваться на ячейке или насколько вероятно то, что нам понадобится доступ к ней. Например, чтобы прочесть вектор на временном шаге t из матрицы памяти N x W , обозначенной M t (где N — число ячеек, а W — размер ячейки), мы создаем вектор внимания, или вектор весов w t размера N , и вектор считывания можно будет вычислить через произведение 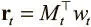 , где
, где 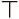 обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.
обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.
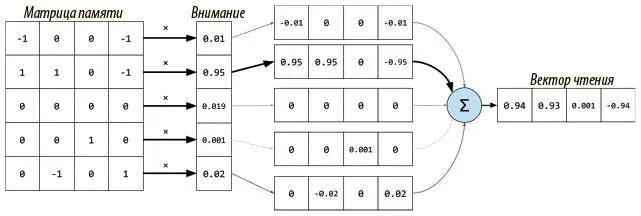
Рис. 8.2. Именно так размытое, основанное на внимании чтение может выдать вектор, содержащий примерно ту же информацию, что и соответствующая ячейка
Тот же метод используется и для головки записи: создается вектор весов w t , который служит для стирания определенной информации из памяти, указанной контроллером вектора стирания e t с W значений от 0 до 1; от этих значений и зависит, что стирать и что хранить. Затем взвешивание проводится для записи в матрицу стертой памяти новой информации, тоже определяемой контроллером в векторе записи v t , которая содержит W значений:
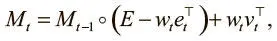
где E — матрица единиц, а ◦ — поэлементное умножение. Как и в случае с чтением, взвешивание w t подсказывает, куда направить операции стирания (первый член уравнения) и записи (второй член).
Механизмы адресации памяти в NTM
Теперь, когда мы понимаем, как NTM способна непрерывно обращаться к памяти при помощи взвешивания внимания, осталось понять, как эти веса порождаются и какие формы обращения к памяти представляют. Для этого стоит проанализировать, что NTM должны делать со своей памятью. Судя по модели, работу которой они имитируют (машина Тьюринга), они должны получать доступ к ячейке по ее значению и уметь двигаться вперед или назад из нее.
Первый способ поведения может быть реализован механизмом доступа, который мы назовем адресацией по содержанию . При такой форме обращения контроллер выдает значение, которое ищет и которое мы будем называть ключом k t , затем определяет степень его сходства с информацией, сохраненной в каждой ячейке, и сосредоточивает внимание на самой похожей из них. Такое взвешивание можно вычислить следующим образом:
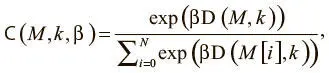
где D — некая мера сходства, например косинусная близость. Это уравнение — нормализованное распределение функции мягкого максимума по результатам сходства. Но здесь есть дополнительный параметр β, призванный при необходимости заставить затухать веса внимания. Мы называем его мощностью ключа. Его основной смысл в том, что для некоторых задач ключ, выданный контроллером, не очень близок к каким-то данным в памяти, что приведет к единообразным с виду весам внимания. На рис. 8.3 показано, как мощность ключа позволяет контроллеру учиться выходить из этой ситуации, чтобы больше сосредоточиваться на одной наиболее вероятной ячейке; затем контроллер учится тому, какое значение мощности выдавать для каждого порождаемого ключа.
Чтобы переходить по памяти вперед-назад, сначала надо понять, где мы сейчас. Эту информацию мы получаем взвешиванием доступа на предыдущем шаге w t−1 . Поэтому, чтобы сохранить информацию о текущем местоположении с новым взвешиванием на основании содержания 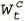 , которое мы только что провели, проводим интерполяцию между двумя взвешиваниями, используя скаляр g t , лежащий между 0 и 1:
, которое мы только что провели, проводим интерполяцию между двумя взвешиваниями, используя скаляр g t , лежащий между 0 и 1:
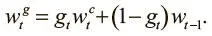
Назовем g tвентилем интерполяции . Он тоже порождается контроллером и контролирует информацию, которую мы хотим использовать на текущем временном шаге. Если значение вентиля близко к 1, мы делаем акцент на обращении по содержанию. Если же оно близко к 0, мы передаем информацию о текущем положении и игнорируем обращение по содержанию. Контроллер учится использовать этот вентиль и, например, может обращать его в 0 при необходимости итерации через последовательные ячейки, когда важнее всего информация о текущем местоположении. Тип информации, которую он пропускает, определяется вентильным взвешиванием 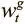 .
.
Интервал:
Закладка:










