Нихиль Будума - Основы глубокого обучения

А если при вычислении взвешивания выделения обнаружится, что все ячейки используются, то есть u t = 1? Тогда все взвешивания обратятся в 0 и в память не поступят новые данные. Потому-то необходимо уметь освобождать и заново использовать память.

Чтобы знать, какие ячейки можно освободить, а какие нет, строим вектор удержания ψ t размера N , который указывает, какое количество данных в каждой ячейке следует сохранить. Каждый элемент принимает значение от 0 до 1, где 0 указывает, что ячейка может быть освобождена, а 1 — что она должна быть полностью сохранена. Вектор вычисляется так:

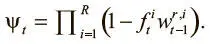
Уравнение сообщает, что уровень, до которого ячейку следует освободить, пропорционален тому, сколько данных прочтено из нее на последних нескольких шагах разными головками (представлены значениями взвешиваний 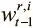). Но постоянное освобождение ячейки памяти сразу после чтения ее данных нежелательно, поскольку эти данные могут нам понадобиться позже.

Оставим контроллеру возможность решить, когда освобождать, а когда сохранять ячейку после прочтения, выдавая набор из R свободных вентилей , значения которых составляют от 0 до 1. Это определяет, насколько нужно освобождать ячейки, на основе того, что их только что прочли. Контроллер обучается использованию этих вентилей для достижения желаемого поведения. Как только вектор удержания получен, можно с его помощью обновить вектор использования, чтобы отражать все освобождения и сохранения:

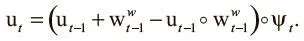
Это уравнение можно прочесть так: ячейка будет использована, если она была сохранена (ее значение ψ t ≈ 1) и либо уже в работе, либо в нее только что произведена запись (о чем свидетельствует значение 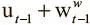). Вычитание поэлементного произведения 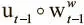возвращает выражение в диапазон между 0 и 1, значение использования вновь становится действительным (если взвешивание записи при предыдущем использовании вышло за пределы 1).

Обновление использования перед вычислением выделения позволяет ввести свободную память для новых данных. Мы теперь также можем более эффективно использовать (впервые или заново) ограниченные ресурсы памяти, преодолевая второе ограничение NTM.

Учитывая динамические механизмы управления памятью, используемые в DNC, каждый раз, когда надо выделить ячейку памяти, мы получаем наименее используемую. Выходит, здесь нет позиционной связи между ней и предыдущей записью. При таком типе доступа к памяти непрерывный способ сохранения временны́х отношений, принятый в NTM, не подходит. Нам нужно вести непосредственную фиксацию порядка записи данных.

В DNC это достигается при помощи еще двух структур данных, дополняющих матрицу памяти и вектор использования. Первая называется вектором предшествования p t . Это вектор размера N, который должен представлять распределение вероятностей по ячейкам, так что каждое значение соответствует вероятности того, что соответствующая ячейка была последней, в которую производилась запись. Предшествование изначально задается равным нулю (p 0 = 0) и обновляется на следующих шагах:

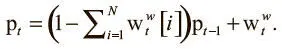
Обновление происходит при первом умножении предыдущих значений предшествования на коэффициент, пропорциональный тому, что только что записано в память (определяется по сумме компонентов взвешивания записи). Затем значение взвешивания добавляется в значение после сброса, и ячейка с большим взвешиванием (та, в которую запись произведена только что) тоже получит высокое значение вектора предшествования.

Вторая структура данных, необходимая для записи временной информации, — матрица ссылок L t . Это матрица размером N x N , в которой элемент L t[i , j] имеет значение от 0 до 1 и показывает, насколько вероятно, что ячейка i была занята после j . На начальном этапе все значения обнулены, а диагональные элементы сохраняются на нулевом уровне в течение времени L t[i , i] = 0, поскольку бессмысленно фиксировать, что ячейка была записана после себя, когда предыдущие данные уже перезаписаны и утрачены. Все остальные элементы в матрице обновляются по такому принципу:

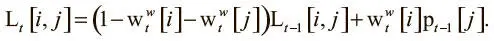
Уравнение создано по тому же шаблону, что и другие правила обновления. Сначала ссылочный элемент сбрасывается при помощи коэффициента, пропорционального уровню записи в ячейки i , j. Затем ссылка обновляется корреляцией (здесь представлена в виде умножения) между взвешиванием записи в ячейке i и предыдущим значением предшествования в j . Так устраняется третье ограничение NTM: мы можем фиксировать временную информацию независимо от того, как головка записи движется по памяти.

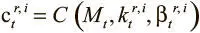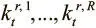Когда головка записи заканчивает обновлять матрицу памяти и соответствующие структуры данных, в игру вступает головка чтения. Ее задача проста: просматривать значения в памяти и проводить итерации вперед и назад по времени между данными. Возможность просмотра достигается простой адресацией по содержанию: для каждой головки записи i мы вычисляем промежуточное значение , где и 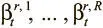— два набора ключей чтения R и мощностей, полученных от контроллера по вектору интерфейса.

Чтобы получить итерации вперед и назад, нужно сделать так, чтобы взвешивания могли делать шаг вперед или назад из ячейки, откуда только что производилось чтение. Для движения вперед это достигается умножением матрицы ссылок на последние прочтенные взвешивания. Это сдвигает веса из последней прочтенной ячейки в ячейку из последней записи, указанной в матрице ссылок, и создает промежуточное переднее взвешивание для каждой головки считывания i : 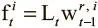. Точно так же создаем и промежуточное заднее взвешивание, умножая транспонированную матрицу ссылок на последние прочтенные взвешивания 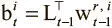. Теперь можно создать новые взвешивания для каждого чтения в соответствии со следующим правилом: