Нихиль Будума - Основы глубокого обучения

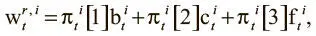
где 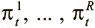— режимы чтения . Это распределения функции мягкого максимума по трем элементам, которые поступают из контроллера вектора интерфейса. Три значения определяют, какое внимание головка чтения должна уделить каждому механизму: заднему, просмотровому и переднему соответственно. Контроллер обучается использовать эти режимы, чтобы указать памяти, как считывать данные.

Теперь, поняв, как работает внешняя память в архитектуре DNC, осталось выяснить, как устроен контроллер, координирующий все операции в памяти. Работа его проста: в его основе лежит нейронная сеть (рекуррентная или с прямым распространением сигнала), которая читает входные данные на текущем шаге вместе с векторами с предыдущего шага и выдает вектор, размер которого зависит от архитектуры сети. Обозначим этот вектор как N(χ t), где N — любая функция, вычисляемая нейронной сетью, а χ t — конкатенация входного вектора на текущем шаге и последних прочитанных векторов 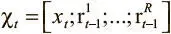. Конкатенация последних прочитанных векторов служит той же цели, что и скрытое состояние в обычной LSTM: связать выходные данные с прошлым. От вектора, исходящего из нейронной сети, нам нужна информация двух видов. Первый — вектор интерфейса ζ t. Как мы уже видели, он содержит всю информацию, чтобы память могла выполнять свою работу. Вектор ζ tможно рассматривать как конкатенацию уже известных отдельных элементов, как показано на рис. 8.7.

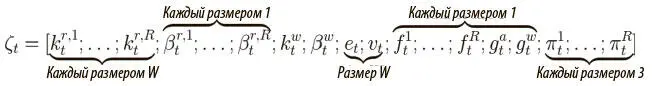
Рис. 8.7. Вектор интерфейса, разложенный на компоненты

Суммируя размеры по компонентам, мы можем считать вектор ζ t как один большой вектор размером ( R × W + 3 W + 5 R + 3). Чтобы получить такой вектор на выводе сети, мы создаем матрицу W ζобучаемых весов |N| × ( R × W + 3 W + 5 R + 3), где |N| — размер выходных данных сети:

ζ t = W ζ N(χt).

Прежде чем передать вектор ζ t в память, надо убедиться, что каждый компонент имеет корректное значение. Например, все вентили и вектор стирания должны составлять от 0 до 1, так что мы пропускаем их через сигмоидную функцию, чтобы обеспечить соответствие этому требованию:

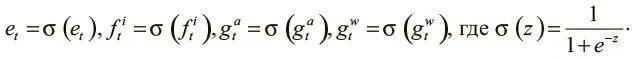
Все просмотровые мощности должны иметь значение не менее 1, так что мы сначала пропускаем их через функцию oneplus :

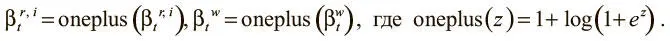
Наконец, режимы чтения должны иметь корректное распределение функции мягкого максимума:

После этих преобразований вектор интерфейса можно передать в память; и пока он руководит операциями, нам нужен второй элемент данных от нейронной сети — предварительная версия выходного вектора v t . Это вектор того же размера, что и окончательный выходной, но им не являющийся. Используя еще одну матрицу W y обучаемых весов |N|× Y , можно получить этот вектор по формуле:

v t = W y N(χ t ).

Он дает возможность связать окончательный выходной вектор не только с выходными данными сети, но и с недавно прочитанными из памяти векторами r t . Из третьей матрицы W r обучаемых весов ( R × W )× Y мы можем получить окончательный выходной вектор:

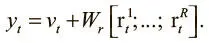
Если контроллер ничего не знает о памяти, кроме размера слова W , обученный контроллер можно масштабировать до большей памяти с большим количеством ячеек без необходимости повторного обучения. Вдобавок то, что нам не пришлось указывать конкретной структуры нейронной сети или конкретной функции потерь, делает DNC универсальным решением, которое можно применить к самому широкому спектру задач обучения.

Один из способов увидеть DNC в деле — обучить его на простой задаче, которая позволит посмотреть на взвешивания и значения параметров и визуализировать их удобным для интерпретации способом. Возьмем проблему копирования, с которой мы уже имели дело при разговоре об NTM, но в несколько видоизмененной форме.

Вместо того чтобы копировать одну последовательность двоичных векторов, мы будем дублировать серии таких последовательностей. На рис. 8.8 (а) показана одна входная последовательность. После ее обработки и копирования на выходе DNC завершил бы свою программу, а его память была бы перезагружена, и нам не удалось бы изучить процесс обработки в динамике. Поэтому мы будем рассматривать ряд последовательностей, показанных на рис. 8.8 (б), как единый ввод.

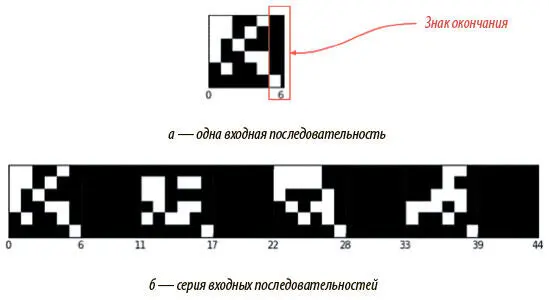
Рис. 8.8. Ввод одной последовательности и серии входных последовательностей

На рис. 8.9 показана визуализация действий DNC, обученного на серии размера 4, где каждая последовательность содержит пять двоичных векторов и знак окончания. Здесь всего 10 ячеек памяти, и все 20 векторов ввода сохранить нельзя. Контроллер с прямым распространением сигнала обеспечивает, чтобы никакие данные не хранились в рекуррентном состоянии, а единственная головка чтения использована для большей наглядности. Эти ограничения должны заставить DNC научиться освобождению и повторному использованию памяти для успешного копирования всего ввода. Так и происходит.

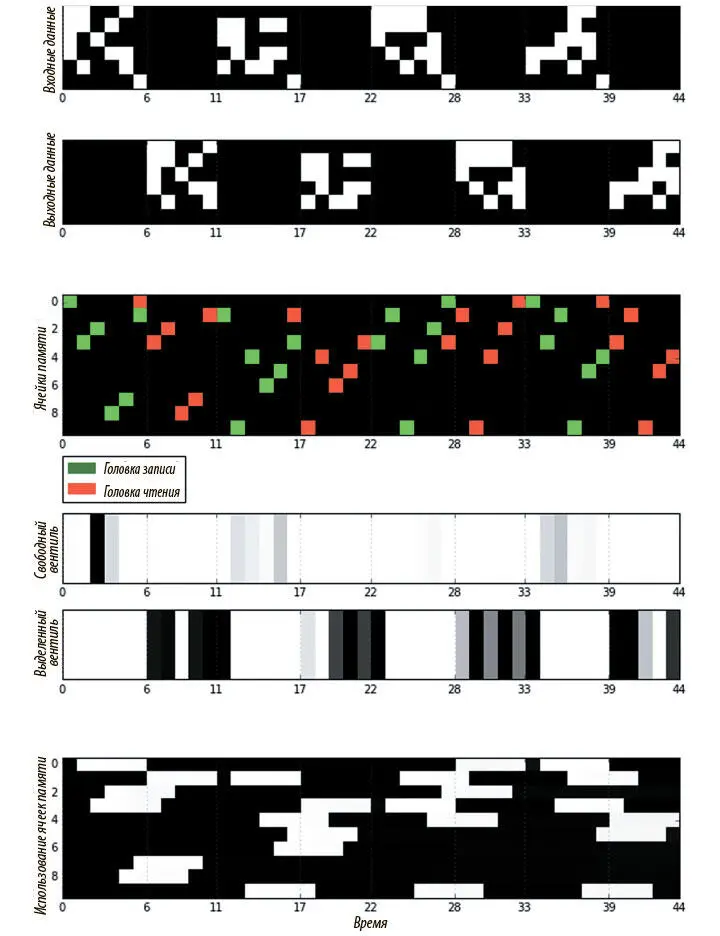
Рис. 8.9. Визуализация работы DNC над проблемой копирования

На визуализации видно, как DNC записывает каждый из пяти векторов последовательности в одну ячейку памяти. После получения знака окончания головка чтения начинает считывать из ячеек в соответствии с порядком записи. Можно видеть, как занятые и свободные вентили чередуют активацию между фазами записи и чтения для каждой последовательности в серии. На графике вектора использования внизу заметно, что после записи в ячейку памяти ее значение использования становится равным 1, а затем снижается до 0 сразу после считывания, показывая, что ячейка освобождена и может быть использована снова.