Нихиль Будума - Основы глубокого обучения

Эта визуализация — часть открытой реализации архитектуры DNC, выполненной Мостафой Самиром [101]. В следующем разделе мы познакомимся с важными приемами, которые позволят нам реализовать более простую версию DNC для работы с проблемой понимания при чтении.

Реализация архитектуры DNC — по сути, прямое применение математики, о которой мы только что говорили. Полная реализация приведена в репозитории кода для этой книги, здесь же мы сосредоточимся на самых трудных местах и попутно расскажем о некоторых новых методах работы с Tensor Flow.

Основная часть реализации находится в файле mem_ops.py : там реализованы все наши механизмы внимания и доступа. Файл импортируется и используется контроллером.

Сложными здесь могут показаться две операции: обновление матрицы ссылок и расчет выделения взвешиваний. Обе можно выполнить наивным способом — с помощью циклов for. Но работа с ними для создания графа вычисления — обычно не лучшая идея. Рассмотрим сначала операцию обновления матрицы ссылок. Вот как она выглядит при цикловой реализации:

def Lt(L, wwt, p, N):

L_t = tf.zeros([N,N], tf.float32)

for i in range(N):

for j in range(N):

if i == j:

continue

_mask = np.zeros([N,N], np.float32);

_mask[i,j] = 1.0

mask = tf.convert_to_tensor(_mask)

link_t = (1 — wwt[i] — wwt[j]) * L[i,j] + wwt[i] * p[j]

L_t += mask * link_t

return L_t

Здесь мы воспользовались уловкой, поскольку TensorFlow не поддерживает назначения для элементов тензоров. Можно понять, что тут не так, если вспомнить, что TensorFlow — образец символического программирования, при котором каждое обращение к API не проводит операцию и не изменяет состояние программы, а определяет узел графа вычислений как символ для операции, которую мы хотим выполнить. После того как граф полностью определен, для него задаются конкретные значения, и он выполняется. Получается, как на рис. 8.10, в большинстве итераций цикла for к графу вычислений добавляется новый набор узлов, соответствующий телу цикла. Поэтому для N ячеек памяти мы получаем ( N 2− N ) идентичных копий одних и тех же узлов — по одной на итерацию.

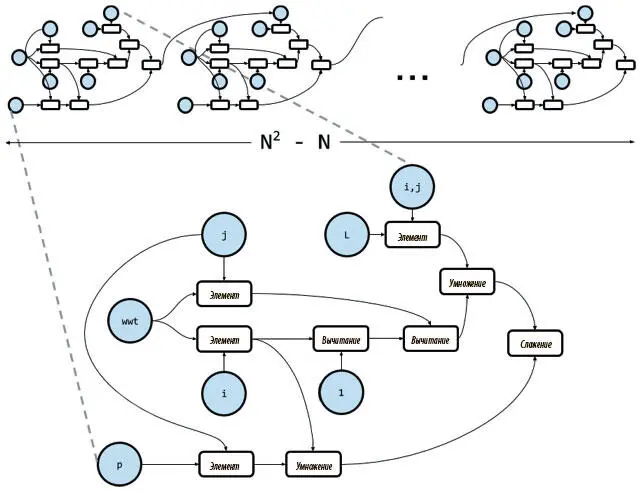
Рис. 8.10. Граф вычислений операции обновления матрицы ссылок, созданный с помощью цикла for

Каждая копия отъедает немного оперативной памяти и времени на обработку. Если N — небольшое число, например 5, получится 20 одинаковых копий, что не так плохо. Но если нам нужна большая память, например N = 256, то будет уже 65 280 одинаковых копий узлов, а это катастрофа и для памяти, и для времени обработки!

Один из способов преодоления этой проблемы — векторизация . Мы выполняем над массивом операцию, которая изначально определяется для конкретных элементов, и перезаписываем ее как операцию над всем массивом. Для обновления матрицы ссылок перезапись может происходить так:

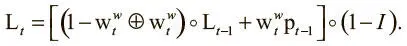
Здесь I — единичная матрица, а 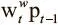— векторное произведение. Чтобы получить векторизацию, мы задаем новый оператор — попарное сложение векторов, обозначаемое ⊕. Его можно определить так:

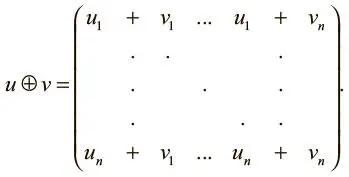
Этот оператор требует дополнительной памяти, но все же не так много, как при цикловой реализации. При векторизованном переформулировании правила обновления мы можем записать более эффективную с точки зрения памяти и времени реализацию:

def Lt(L, wwt, p, N):

# we only need the case of adding a single vector to itself (нам нужен только случай добавления единичного вектора к самому себе)

def pairwise_add(v):

n = v.get_shape(). as_list()[0]

# an NxN matrix of duplicates of u along the columns (матрицы NxN копий u по столбцам)

V = tf.concat(1, [v] * n)

return V + V

I = tf.constant(np.identity(N, dtype=np.float32))

updated = (1 — pairwise_add(wwt)) * L + tf.matmul(wwt, p)

updated = updated * (1 — I) # eliminate self-links

return updated

Примерно то же можно сделать и для правила выделения взвешиваний. Одно правило для каждого элемента вектора мы разбиваем на несколько операций, которые будут работать со всем вектором сразу.

1. При сортировке вектора использования для получения списка свободной памяти берем также сам вектор отсортированного использования.

2. Вычисляем вектор кумулятивного произведения отсортированного использования. Каждый элемент соответствует части произведения в первоначальном поэлементном правиле.

3. Умножаем вектор кумулятивного произведения на (1-вектор отсортированного использования). Полученный вектор — выделение взвешивания, но в отсортированном порядке, а не в исходном порядке ячейки записи.

4. Для каждого элемента неупорядоченного выделения взвешивания берем его значение и помещаем в соответствующий индекс списка свободной памяти. Полученный вектор — то выделение взвешивания, которое нам и нужно.

На рис. 8.11 приведен этот же процесс с числовыми примерами.

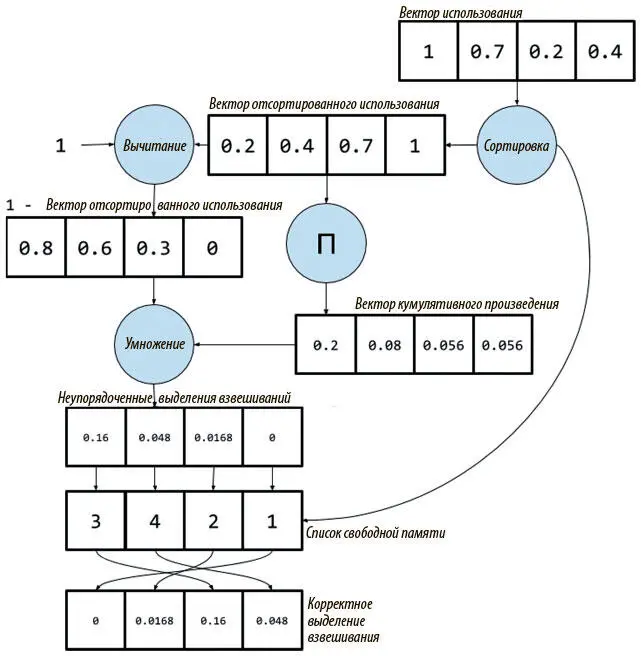
Рис. 8.11. Векторизованный процесс расчета выделения взвешивания

Может показаться, что для сортировки на шаге 1 и переупорядочивания весов на шаге 4 нам все равно понадобятся циклы, но, к счастью, TensorFlow предлагает такие символические операции, которые позволяют выполнять эти действия, не прибегая к циклам Python.

Для сортировки мы будем использовать tf.nn.top_k. Эта операция принимает тензор и число k и выдает как отсортированные высшие значения k в порядке убывания, так и их индексы. Чтобы получить вектор отсортированного использования в порядке возрастания, нужно взять высшие значения N вектора, обратного вектору использования. Привести отсортированные значения к исходным знакам можно, умножив получившийся вектор на −1:

sorted_ut, free_list = tf.nn.top_k(-1 * ut, N)

sorted_ut *= -1

Для переупорядочивания весов выделения воспользуемся новой структурой данных TensorFlow под названием TensorArray. Эти массивы можно считать символической альтернативой списку Python. Сначала получаем пустой массив тензоров размера N, содержащий веса в верном порядке, затем помещаем туда значения в правильном порядке методом экземпляра scatter(indices, values). Он получает в качестве второго аргумента тензор и рассеивает значения по первому измерению по всему массиву, причем первый аргумент — список индексов ячеек, по которым мы хотим рассеять соответствующие значения. В нашем случае первый аргумент — список свободной памяти, а второй — неупорядоченные выделения взвешиваний. Получив массив с весами в нужных местах, используем еще один метод экземпляра — pack() — для помещения всего массива в объект Tensor: