Нихиль Будума - Основы глубокого обучения

( s 0, a 0, r 0), ( s 1, a 1, r 1), … ( s n, a n, r n ).

В примере с тележкой (cart) и шестом (pole) состояние среды может быть кортежем из положения тележки и угла шеста, например: ( x cart , θ pole ).

Цель MDP — найти оптимальную стратегию для агента. Стратегия — способ действия в зависимости от текущего состояния. Формально ее можно представить в виде функции π , которая выбирает действие a , выполняемое агентом в состоянии s . Цель MDP — найти стратегию максимального увеличения ожидаемой будущей выгоды: max πE[R 0 + R 1 +…R t|π]. Здесь R отражает будущую выгоду от каждого эпизода. А теперь дадим ее более строгое определение.

Будущая выгода — ожидаемые вознаграждения. Выбор оптимального действия требует учитывать не только непосредственные результаты, но и долгосрочные последствия. Например, агент-альпинист, получающий вознаграждения за достижение высоты, может решить немного спуститься, чтобы перейти на более удобный путь к вершине горы.

Мы хотим, чтобы наши агенты были оптимизированы в отношении будущей выгоды . Для этого им стоит учитывать отдаленные последствия своих действий. Например, в пинг-понге агент получает вознаграждение, когда соперник не может отбить его удар. Но действия, ведущие к этому (входные данные, которые обусловили положение ракетки, позволяющее нанести решающий удар), происходят за много шагов до получения вознаграждения, и его стоит считать отложенным.

Мы можем включить отложенные вознаграждения в общий сигнал, создав выгоду для каждого шага, которая будет учитывать как немедленные, так и будущие вознаграждения. Наивный подход к вычислению будущей выгоды на данном шаге — простая сумма вроде следующей:

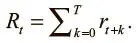
Мы можем вычислить все выгоды, R , где R = { R 0, R 1,… R i ,… R n }, с помощью следующего кода:

def calculate_naive_returns(rewards):

""" Calculates a list of naive returns given a

list of rewards.""" (Вычисляет список наивных выгод на основании списка вознаграждений)

total_returns = np.zeros(len(rewards))

total_return = 0.0

for t in range(len(rewards), 0):

total_return = total_return + reward

total_returns[t] = total_return

return total_returns

Этот подход включает будущие выгоды, и агент может научиться оптимальной общей стратегии. Здесь будущие выгоды ценятся так же, как и немедленные. Но это-то и беспокоит. При бесконечном числе шагов это выражение может свестись к бесконечности, так что нужно установить для него предел. Более того, если на каждом этапе все выгоды расценивать одинаково, агент может оптимизировать действия для очень отдаленной выгоды, и получится стратегия, в которой не учитываются срочность или иной вариант зависимости вознаграждения от времени.

Поэтому следует оценивать будущие вознаграждения чуть ниже, чтобы наши агенты могли научиться получать их быстрее. Этого можно достичь с помощью дисконтирования будущих выгод .

Для реализации этого подхода мы умножаем вознаграждение текущего состояния на коэффициент дисконтирования γ в степени текущего шага. Тем самым мы штрафуем агентов, которые совершают много действий до получения положительного вознаграждения. Благодаря дисконтированию наш агент будет выбирать вознаграждения в недалеком будущем, что позволит развить хорошую стратегию. Это вознаграждение можно выразить так:

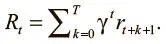
Коэффициент дисконтирования γ отражает уровень снижения, которого мы хотим достичь, и может принимать значение от 0 до 1. Высокий γ соответствует небольшому дисконтированию, низкий — значительному. Типичное значение гиперпараметра γ — между 0,99 и 0,97.

Реализовать дисконтирование выгоды можно так:

def discount_rewards(rewards, gamma=0.98):

discounted_returns = [0 for _ in rewards]

discounted_returns[-1] = rewards[-1]

for t in range(len(rewards)-2, -1, -1): # iterate backwards

discounted_returns[t] = rewards[t] +

discounted_returns[t+1]*gamma

return discounted_returns

Обучение с подкреплением — по сути, метод проб и ошибок. В таких условиях агент, опасающийся провала, будет не очень-то эффективен. Рассмотрим такой сценарий. Мышь помещают в лабиринт, показанный на рис. 9.5. Агент должен управлять ею для получения максимального вознаграждения. Если мышь находит воду, она получает +1; если контейнер с ядом (красный), то –10; за нахождение сыра дается +100. После вознаграждения эпизод заканчивается. Оптимальная стратегия должна помочь мыши успешно добраться до сыра и съесть его.

Рис. 9.5. Ситуация, в которой оказываются многие мыши

В первом эпизоде мышь идет влево, попадает в ловушку и получает –10. Во втором она избегает движения налево, поскольку результат оказался отрицательным, сразу выпивает воду, находящуюся справа, и получает +1.

После двух эпизодов может показаться, что мышь нашла хорошую стратегию. Животное продолжает и дальше следовать ей и получает скромную, но гарантированную награду +1. Поскольку агент следует жадной стратегии, всегда выбирая лучшее действие в модели, он оказывается в ловушке локального максимума .

Чтобы предотвратить такие ситуации, агенту полезно отклониться от рекомендации модели и выбрать неоптимальное действие, чтобы лучше исследовать среду.

Вместо того чтобы сразу сделать шаг направо и использовать среду, получив воду и гарантированные +1, агент может однажды шагнуть налево и отправиться в более опасные области в поисках лучшей стратегии. Однако чрезмерное исследование приведет к отсутствию награды. Недостаточные же приведут в ловушку локального максимума. Такой баланс исследования и использования необходим для обучения успешной стратегии.

Стратегия уравновешивания дилеммы исследования и использования называется ϵ- жадностью . Это простая стратегия, связанная с выбором на каждом шаге между наиболее рекомендуемым действием и каким-нибудь случайным.

Вероятность того, что агент предпочтет случайное действие, определяется значением ϵ.

Реализовать стратегию ϵ-жадности можно так:

def epsilon_greedy_action(action_distribution, epsilon=1e-1):

if random.random() < epsilon:

return np.argmax(np.random.random(

action_distribution.shape))

else:

return np.argmax(action_distribution)

При обучении модели с подкреплением вначале мы часто хотим выбрать исследование, поскольку наша модель мало знает мир. Потом, когда она хорошо познакомится со средой и научится хорошей стратегии, нам будет желательно, чтобы агент больше доверял себе, — это приведет к дальнейшей оптимизации стратегии. И мы отказываемся от идеи фиксированного ϵ и периодически нормализуем его со временем, начиная с небольшого значения и после каждого эпизода обучения увеличивая его на какой-то коэффициент. Типичные условия нормализованных сценариев ϵ-жадности включают нормализацию с 0,99 до 0,1 за 10 тысяч подходов. Реализовать нормализацию можно так: