Нихиль Будума - Основы глубокого обучения

Задаем функцию predict_action, которая семплирует действие на основании выходного распределения вероятностей действия модели. Мы поддерживаем разные стратегии семплирования, о которых говорилось выше, чтобы достичь равновесия исследования и использования, в том числе жадную, ϵ-жадную и нормализованную ϵ-жадную стратегии.

Мы будем объединять градиенты запусков множества эпизодов, так что полезно будет записывать кортежи состояния, действия и вознаграждения. Для этого реализуем историю и память эпизода.

class EpisodeHistory(object):

def __init__(self):

self.states = []

self.actions = []

self.rewards = []

self.state_primes = []

self.discounted_returns = []

def add_to_history(self, state, action, reward,

state_prime):

self.states.append(state)

self.actions.append(action)

self.rewards.append(reward)

self.state_primes.append(state_prime)

class Memory(object):

def __init__(self):

self.states = []

self.actions = []

self.rewards = []

self.state_primes = []

self.discounted_returns = []

def reset_memory(self):

self.states = []

self.actions = []

self.rewards = []

self.state_primes = []

self.discounted_returns = []

def add_episode(self, episode):

self.states += episode.states

self.actions += episode.actions

self.rewards += episode.rewards

self.discounted_returns += episode.discounted_returns

Соединим всё это в нашей основной функции, которая создаст среду OpenAI Gym для примера CartPole (тележка с шестом), задаст пример агента и заставит его взаимодействовать со средой CartPole и обучаться на ней.

def main(argv):

# Configure Settings (Конфигурируем настройки)

total_episodes = 5000

total_steps_max = 10000

epsilon_stop = 3000

train_frequency = 8

max_episode_length = 500

render_start = -1

should_render = False

explore_exploit_setting =

‘epsilon_greedy_annealed_1.0->0.001'

env = gym.make(‘CartPole-v0')

state_size = env.observation_space.shape[0] # 4 for

# CartPole-v0

num_actions = env.action_space.n # 2 for CartPole-v0

solved = False

with tf.Session() as session:

agent = PGAgent(session=session, state_size=state_size,

num_actions=num_actions,

hidden_size=16,

explore_exploit_setting=

explore_exploit_setting)

session.run(tf.global_variables_initializer())

episode_rewards = []

batch_losses = []

global_memory = Memory()

steps = 0

for i in tqdm.tqdm(range(total_episodes)):

state = env.reset()

episode_reward = 0.0

episode_history = EpisodeHistory()

epsilon_percentage = float(min(i/float(

epsilon_stop), 1.0))

for j in range(max_episode_length):

action = agent.predict_action(state,

epsilon_percentage)

state_prime, reward, terminal, _ =

env.step(action)

if (render_start > 0 and i >

render_start and should_render) \

or (solved and should_render):

env.render()

episode_history.add_to_history(

state, action, reward, state_prime)

state = state_prime

episode_reward += reward

steps += 1

if terminal:

episode_history.discounted_returns =

discount_rewards(

episode_history.rewards)

global_memory.add_episode(

episode_history)

if np.mod(i, train_frequency) == 0:

feed_dict = {

agent.reward_input: np.array(

global_memory.discounted_returns),

agent.action_input: np.array(

global_memory.actions),

agent.state: np.array(

global_memory.states)}

_, batch_loss = session.run(

[agent.train_step, agent.loss],

feed_dict=feed_dict)

batch_losses.append(batch_loss)

global_memory.reset_memory()

episode_rewards.append(episode_reward)

break

if i % 10:

if np.mean(episode_rewards[:-100]) > 100.0:

solved = True

else:

solved = False

Этот код обучит агента CartPole успешно и надежно удерживать шест в равновесии.

Рисунок 9.6 — таблица средних вознаграждений нашего агента на каждом шаге обучения. Мы пробуем восемь разных методов семплирования, а лучший результат достигается при помощи нормализованной ϵ-жадной стратегии (от 1 до 0,001).

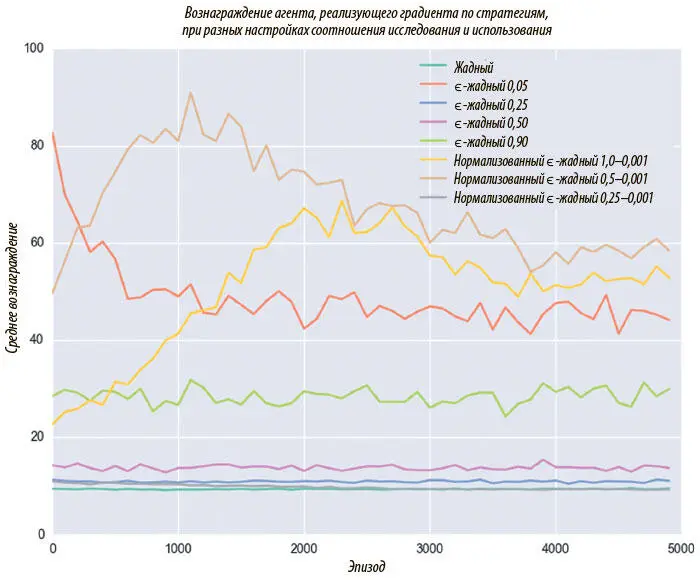
Рис. 9.6. Конфигурация соотношения исследования и использования влияет на скорость и успешность обучения

Отметим, что в целом стандартный ϵ-жадный алгоритм дает очень плохие результаты. Обсудим, почему так происходит. Если задано верхнее значение ϵ = 0,9, мы совершаем случайные действия 90% времени.

Даже если модель научится выполнять идеальные действия, это будет использовано всего в 10% случаев. А вот если значение ϵ низкое — 0,05, мы в подавляющем большинстве случаев совершаем действия, которые модель считает оптимальными. Эффективность выше, но велика вероятность скатиться к локальному максимуму вознаграждения, поскольку почти нет возможности исследовать другие стратегии.

Итак, ϵ-жадный алгоритм не дает хороших результатов ни при 0,05, ни при 0,9: исследованию уделяется либо слишком много, либо слишком мало внимания. Вот почему нормализация ϵ оказывается хорошей стратегией семплирования. Она позволяет модели сначала исследовать, а затем использовать, что необходимо для изучения хорошей стратегии.

Q-обучение — категория модели с подкреплением, именуемая обучением ценности. Вместо непосредственного исследования стратегии мы будем усваивать ценности состояний и действий.

Q-обучение связано с исследованием Q-функции , которая отражает качество пары (состояние, действие). Q(s, a) — функция, которая рассчитывает максимальную дисконтированную будущую выгоду от совершения действия a в состоянии s.

Значение Q отражает ожидаемые долгосрочные выгоды, если мы в соответствующем состоянии и совершаем соответствующее действие, а затем идеально выполняем все последующие (чтобы получить максимальную ожидаемую будущую выгоду). Формально это можно выразить так:

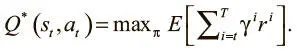
Возможно, вы задаетесь вопросом: как узнать значения Q? Ведь даже людям тяжело понять, насколько хорошо то или иное действие, поскольку надо знать, как вы собираетесь поступать в будущем. Ожидаемые выгоды зависят от нашей долгосрочной стратегии. Это похоже на проблему курицы и яйца: чтобы оценить пару (состояние, действие), нужно знать все идеальные дальнейшие действия. А чтобы знать, какие будущие действия окажутся идеальными, нужно иметь точно рассчитанные стоимости состояния и действия.

Мы решаем эту дилемму, определяя значения Q как функцию от будущих значений Q. Такие отношения называются уравнением Беллмана, которое утверждает, что максимальная будущая выгода от действия a — текущая выгода плюс максимальная будущая на следующем шаге от совершения следующего действия a':

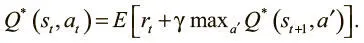
Это рекурсивное определение позволяет установить соответствие между значениями Q в прошлом и будущем, и уравнение удобно задает правило обновления. Мы можем обновить предыдущие значения Q так, чтобы они основывались на будущих. И здесь очень удачно, что мы точно знаем одно верное значение Q: это Q для самого последнего действия перед окончанием эпизода.

Для этого состояния мы точно знаем, что следующее действие привело к новому вознаграждению, и можем точно задать значения Q. Теперь можно использовать правило обновления для распространения этого значения на предыдущий шаг: