Нихиль Будума - Основы глубокого обучения

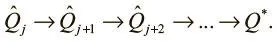
Такое обновление называется итерацией по значениям .

Первое значение Q оказывается неверным, но это приемлемо. С каждой итерацией мы можем обновлять его при помощи верного значения в будущем. После одной итерации последнее значение Q верно, ведь это вознаграждение с последнего состояния и действия перед окончанием эпизода. Затем мы проводим обновление Q и устанавливаем тем самым его значение для второй с конца пары (состояние, действие). На следующей итерации мы можем гарантировать, что верны два последних значения Q, и т. д. Благодаря итерации по значениям гарантируется схождение к конечному оптимальному значению Q.

Итерация по ценностям устанавливает связь между парами состояний и действий и значениями Q, и мы создаем таблицу этих связей, которая называется Q-таблицей .

Коротко поговорим о ее размере. Итерация по ценностям — утомительный процесс, который требует полного обхода всех пар (состояние, действие). Например, в игре Breakout 100 кирпичиков могут либо присутствовать, либо нет, а также есть 50 возможных положений ударной лопатки, 250 возможных позиций шарика и три действия — и уже здесь такой объем, который во много раз превосходит сумму всех вычислительных возможностей человечества. А в стохастических средах объем Q-таблицы будет еще больше — возможно, даже бесконечным. И тогда найти Q-значения всех пар (действие, состояние) станет невозможно. Этот подход явно не сработает. Как же тогда заниматься Q-обучением?

Размер Q-таблицы делает наивный подход неосуществимым для любой реальной задачи. Но что если ослабить требования к оптимальной Q-функции? Если обучать аппроксимацию Q-функции, можно использовать модель для ее оценки.

Вместо того чтобы пытаться исследовать каждую пару (состояние, действие) ради обновления Q-таблицы, можно обучить функцию, которая будет аппроксимировать ее и даже строить обобщения за пределами своего опыта. И нам не придется вести утомительный поиск по всем возможным Q-значениям для обучения функции.

Этим руководствовались в DeepMind при работе над глубокой Q-сетью (Deep Q-Network, DQN). DQN берет глубокую нейронную сеть, которая на основе полученного изображения (состояния) оценивает Q-значение для всех возможных действий.

Мы хотим обучить сеть аппроксимировать Q-функции. Выразим ее аппроксимацию как функцию параметров нашей модели:

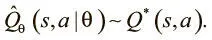
Помните, что Q-обучение — это обучение ценности. Мы осваиваем не саму стратегию, а ценность каждой пары (действие, состояние), независимо от их качества. Аппроксимацию Q-функции нашей модели мы выразили как Qtheta, и мы хотели бы, чтобы она была близка к ожидаемому вознаграждению. Используя уравнение Беллмана, рассмотренное выше, мы можем выразить его так:

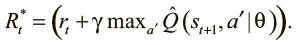
Наша цель — минимизировать разницу между аппроксимацией Q и следующим значением Q:

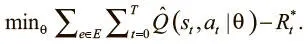
Раскрытие этого выражения дает нам полную целевую функцию:

Она полностью дифференцируема как функция параметров нашей модели, и можно найти для нее градиенты для использования в стохастическом градиентном спуске и минимизации потерь.

Вы наверняка уже заметили проблему: мы определяем функцию потерь на основе разницы предсказанного Q-значения нашей модели для этого шага и для следующего. Получается, потери вдвойне зависят от параметров модели.

При каждом обновлении параметров Q-значения сдвигаются, а мы используем их для дальнейших обновлений. Высокая корреляция обновлений может привести к циклам обратной связи и нестабильности в обучении, поскольку параметры порой значительно колеблются и функция потерь не сходится.

Чтобы устранить эту проблему корреляции, можно использовать пару простых инженерных хитростей: это целевая Q-сеть и воспроизведение опыта.

Вместо постоянного обновления одной сети по отношению к самой себе можно снизить взаимозависимость, введя вторую, которая называется целевой. Наша функция потерь относится к случаям Q-функци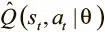и, и .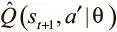

Мы представим первое Q как предсказательную сеть, а второе будет выдаваться целевой Q-сетью. Последняя — копия предсказательной сети с задержкой обновления параметров.

Мы обновляем целевую Q-сеть в соответствии с предсказательной только через каждые несколько пакетов. Это дает необходимую стабильность Q-значениям, и теперь можно должным образом изучить хорошую Q-функцию.

Есть еще один источник досадной нестабильности в обучении: высокие корреляции последних действий. Если обучать DQN на пакетах из недавнего опыта, все пары (состояние, действие) будут взаимосвязаны. Это вредно, поскольку мы хотим, чтобы градиенты пакета представляли весь градиент; а если данные нерепрезентативны для распределения данных, пакетный градиент не будет точным приближением истинного.

Поэтому нам нужно разбить корреляцию данных в пакетах. Это можно осуществить при помощи повторения опыта . Мы сохраняем весь опыт агента в таблице, а чтобы создать пакет, проводим случайную выборку. Опыт хранится в таблице в виде кортежей ( s i, a i, r i, s i + 1). Из этих четырех значений можно вычислить функцию потерь, а с ней и градиент для оптимизации сети.

Таблица воспроизведения опыта больше похожа на очередь. Опыт, который агент получил на ранних стадиях обучения, может не отражать тот, с которым сталкивается уже обученный агент, так что полезно время от времени удалять очень старый опыт из таблицы.

Q-обучение — парадигма обучения ценностям, а не алгоритм освоения стратегии. Мы не обучаем прямо стратегию действия в среде. А можем ли мы разработать ее на основе данных Q-функции? Если мы нашли хорошую аппроксимацию, мы знаем ценность каждого действия для каждого состояния. И теперь можно тривиально выработать оптимальную стратегию: просмотреть Q-функцию на предмет всех действий в текущем состоянии, выбрать действие с максимальным значением Q, перейти в новое состояние и повторить то же. Если Q-функция оптимальна, выработанная на ее основе стратегия тоже будет оптимальной. И тогда мы можем выразить оптимальную стратегию так: