Нихиль Будума - Основы глубокого обучения

• Вектор интерфейса , который содержит всю необходимую информацию для запроса в память (то есть записи и чтения).

• Предварительную версию выходного вектора размером Y.

Внешняя память принимает вектор интерфейса, проводит необходимую запись единственной головкой и читает R новых векторов из памяти. Она выдает только что прочитанные векторы в контроллер, где те суммируются с предварительным выходным вектором. Получается итоговый выходной вектор размером Y .

На рис. 8.6 наглядно показана работа DNC, которую мы только что описали. В отличие от NTM, DNC сохраняют и остальные структуры данных вместе с памятью, что позволяет отслеживать ее состояние. Как мы вскоре увидим, благодаря этим структурам и новым разумным механизмам внимания DNC способны успешно преодолеть ограничения NTM.

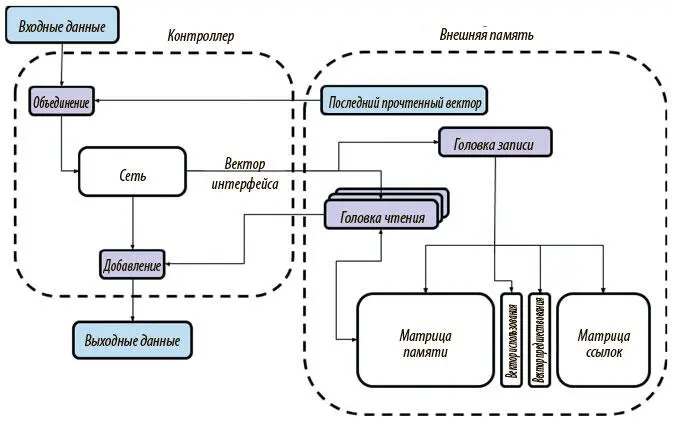
Рис. 8.6. Обзор архитектуры и схемы работы DNC. Внешняя память DNC отличается от NTM несколькими дополнительными структурами данных, а также механизмами внимания, используемыми для доступа

Чтобы архитектура была дифференцируемой, DNC получают доступ к памяти через вектора весов размера N , элементы которых определяют, насколько головки концентрируются в каждой ячейке. Имеется R взвешиваний для головок чтения 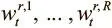, где t обозначает временной шаг. И есть одно взвешивание записи 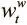для единственной головки. Получив эти взвешивания, можно внести обновления в матрицу памяти:

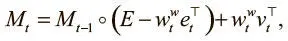
где e t, v t — векторы стирания и записи , которые нам уже знакомы по NTM и поступают от контроллера по вектору интерфейса как указания о том, что стереть из памяти и что в нее записать.

Получив обновленную матрицу M t , мы можем прочесть новые векторы считывания 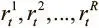при помощи следующего уравнения для каждого взвешивания:

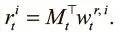
Пока создается впечатление, что в процедуре записи и считывания DNC и NTM все шаги совпадают. Разница станет заметна, когда мы перейдем к разбору механизмов внимания, используемых в DNC для получения этих взвешиваний. Обе машины используют механизм адресации по содержанию C(M, k, β), о котором шла речь выше, но механизмы DNC более совершенны; более эффективно и обращение к памяти.

Первое ограничение NTM, о котором мы говорили, — невозможность обеспечить запись без помех. Интуитивный способ решения этой проблемы — разработать архитектуру, которая будет жестко концентрироваться на единственной свободной ячейке памяти, не дожидаясь, пока NTM научится это делать. Чтобы следить, какие ячейки свободны, а какие заняты, нам нужна новая структура данных, способная удерживать информацию такого рода. Назовем ее вектором использования . Вектор использования u t — вектор размера N , где каждый элемент имеет значение от 0 до 1. Это отражает степень использования соответствующей ячейки памяти: 0 — полностью свободная, 1 — полностью занятая. Вектор использования изначально содержит нули u 0 = 0и обновляется на каждом шаге при появлении информации. Благодаря ей становится ясно, что ячейка, на которую нужно обратить особое внимание, имеет наименьшее значение использования. Чтобы получить такое взвешивание, нужно отсортировать вектор использования и получить список индексов ячеек в восходящем порядке. Такой список называется свободным , обозначим его как ϕ t . Благодаря ему можно создать промежуточное взвешивание — взвешивание выделения a t , которое определяет, какая ячейка памяти отводится под новые данные. Вычисляется a t так:

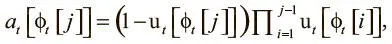
где j ∈ 1,…, N .

На первый взгляд, уравнение кажется непонятным. Его проще осознать, если взять числовой пример. Пусть u t = [1, 0.7, 0.2, 0.4]. Расчеты вы сможете провести сами. В итоге у вас должно получиться такое взвешивание выделения: a t = [0, 0.024, 0.8, 0.12]. После вычислений становится ясно, как работает формула: 1 − u t [ϕ t [ j ]] делает вес ячейки пропорциональным степени ее незанятости. Отметим, что произведение 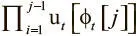становится все меньше при итерациях по свободному списку, поскольку мы постоянно перемножаем числа из множества от 0 до 1. Оно дополнительно снижает вес ячейки при переходе от наименее используемой ячейки к наиболее используемой. В результате самая свободная ячейка получает наибольший вес, а самая занятая — наименьший. Так мы можем гарантировать способность сосредоточиваться на одной ячейке, не рассчитывая, что модель научится этому с нуля: отсюда большая надежность и сокращение времени обучения.

Имея взвешивание выделения a t и взвешивание просмотра 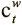, которые мы получаем из механизма адресации по содержанию: 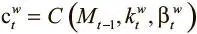, где 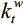, 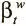— ключ и сила просмотра, полученные по вектору интерфейса, можно вывести итоговое взвешивание записи:

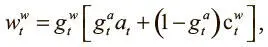
где 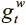, 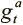— значения от 0 до 1, именуемые вентилем записи и вентилем выделения, которые мы тоже получаем из контроллера через вектор интерфейса. Вентили контролируют операцию записи, причем 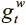сначала определяет, должна ли вообще делаться запись, а 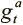показывает, будем ли мы добавлять информацию в новую ячейку при помощи взвешивания выделения или изменим текущее значение, указанное просмотровым взвешиванием.