Алексей Геращенко - Экономика ХХІ

Налоги на фонд оплаты труда. Единый социальный взнос с предприятия = 20 × 40 % = 8 тысяч гривен. Ставка 40 % взята как средняя, она зависит на практике от группы риска работников предприятия.

Налоги с сотрудников.

Единый социальный взнос = 3,6 % × 20 = 720 гривен.

Военный сбор = 1,5 % × (20 – 0,72) = 192 гривны.

Налог на доходы физических лиц = (20 – 0,72) × 15 % = 1,92 тысячи.

Таким образом, зарплата на руки составит: 20 – 0,72 – 0,192 – 1,92 = 17168 гривен.

А сумма всех уплаченных налогов составит 0,72 + 0,192 + 1,92 + 8 = 10832 гривен.

Как видим, налоговая нагрузка на фонд оплаты труда – очень значительная.

Ожидается реформирование и снижение налоговой нагрузки на доходы граждан в 2016 году.

Прибыль = 75 (доходы без НДС) – 25 (стоимость материалов без НДС) – 28 (фонд оплаты труда со всеми налогами) – 5 (транспортировка) – 2 (амортизация) – 8 (другие затраты) = 7 тысяч гривен.

Налог на прибыль = 7 × 18 % = 1,26 тысяч.

Чистая прибыль = 7–1,26 = 5,74 тысяч гривен.

По основным налогам уплачено 10 + 10,832 + 1,26 = 22,1 тысячи гривен.

Взгляните на это соотношение чистой прибыли и уплаченных налогов. Если вам показалось, что налоги чересчур высоки и справедливей было бы недоплатить их и получить немного больше прибыли, то вы сделали первый шаг на пути к налоговой оптимизации. Остановились бы вы на законных методах оптимизации налогообложения (например, предложили бы сотрудникам стать частными предпринимателями с упрощённой системой налогообложения и оплачивали бы их услуги) или пошли бы дальше, кто знает, не так ли?

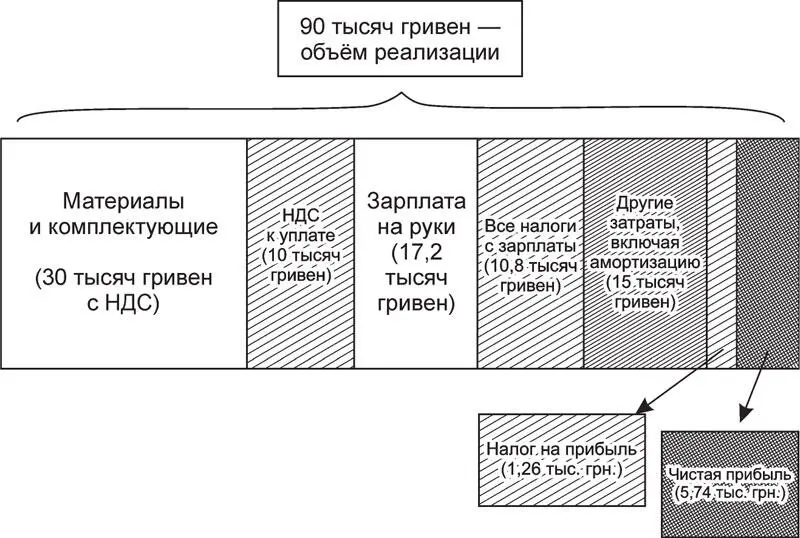
Налоги в структуре финансовых показателей деятельности предприятия

Концепция стоимости денег во времени пронизывает понимание множества экономических процессов. Движение капиталов в мире и внутри страны, решение об инвестициях, приоритет краткосрочным или длительным проектам, оценка стоимости бизнеса и многое другое.

Эволюция человеческого мозга длится уже миллионы лет, а экономическими расчётами человек занялся сравнительно недавно. Поэтому некоторые функции и оценки мы производим практически автоматически, сами не понимаем, как это происходит. А другие, среди которых и финансовые расчёты, для множества людей представляют реальную проблему.

Концепция стоимости денег во времени не является интуитивно понятной. Потребуются определённые усилия, чтобы принять её логику. Тем не менее, она весьма важна, а её методы и механизмы являются своего рода стандартом коммуникации в современной экономике.

Финансы – это своего рода язык, благодаря которому люди в разных уголках земного шара могут понять друг друга. В современном мире, когда экономика стирает границы отношений, это крайне важно.

Представьте себе, что положили в банк 1000 гривен под 20 % годовых на 1 год. Через год вы будете обладать суммой 1200 гривен. А что, если вы оставите эту сумму ещё на год? Тогда проценты будут начисляться на общую сумму 1200 и составят 1200 × 20 % = 240 гривен. А общая сумма вклада будет 1200 + 240 = 1440 гривен.

Если проследить, что будет происходить с суммой вклада и процентами, то получим такую последовательность относительно общей суммы, которой мы владеем:

Рост суммы вклада при реинвестировании процентов (ставка = 20 % годовых):

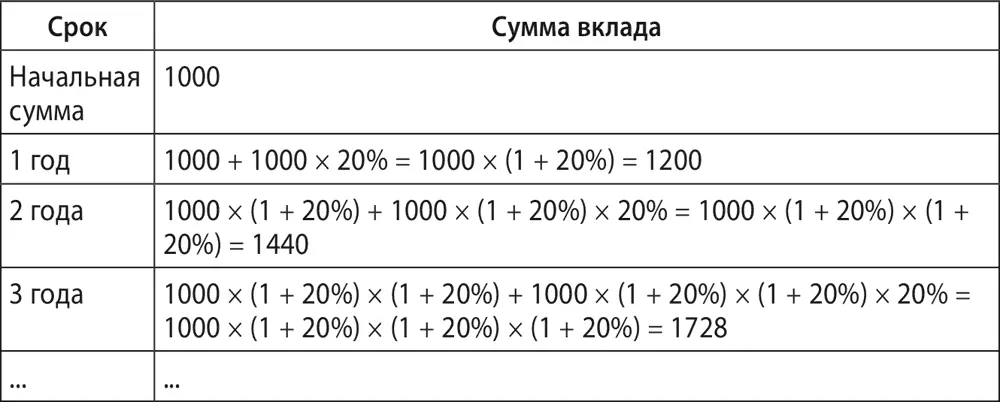
Наблюдая за ростом суммы на вкладе, можно прийти к такой закономерности: при реинвестировании процентов по вкладу сумма на конец периода будет составлять

где S – сумма вклада на конец периода;

S0 – начальная сумма вклада;

w – ставка процента, под которую инвестирована сумма S0;

t – период времени (срок) вклада.

Это так называемая формула сложных процентов. Чтобы посчитать, какой суммой мы будем обладать через 5 лет, подставляем значения в формулу:

S = 1000 × (1 + 20 %) 5= 2488,32 гривен.

А через 100 лет?

S = 1000 × (1 + 20 %) 100= 82817974522 гривен (более 82 миллиардов гривен).

Впечатляет, не так ли? Сложные проценты на длительных временных отрезках выдают настолько впечатляющие цифры, что люди порой отказываются им верить. Например, если бы в момент рождения Иисуса Христа мы положили бы 1 цент под 5 % годовых, то через 2015 лет имели бы цифру с сорока нулями после запятой. Здесь своего рода проблема нашего мышления и восприятия. Мы мыслим сегодняшними деньгами и изначально невыполнимую установку об одном центе воспринимаем как данность.

Из категории сложных процентов возникают другие экономические последствия, а именно:

1. Деньги под матрасом или в тумбочке теряют свою стоимость. Когда деньги не попадают в экономику, вы утрачиваете альтернативную доходность.

2. Процентные ставки, как мы помним, зависят от уровня риска. Поэтому в рискованной ситуации, на рисковой территории вы должны предложить потенциальному инвестору действительно высокую отдачу на инвестиции в будущем, ведь иначе он предпочтёт другие альтернативы.

3. Небольшие преимущества преумножаются и дают весомый эффект благодаря мультипликативному эффекту сложного процента.

4. Чрезмерно высокие ставки существенно ограничивают число проектов, претендующих на финансирование в силу того, что не способны дать высокий ожидаемый эффект.

Также приведём пример того, как банки могут использовать недостаточное знание людей о работе сложного процента. Например, банк предлагает альтернативу – положить деньги на вклад под 25 % годовых с начислением процентов в конце срока или сделать вклад с ежемесячным начислением процентов по 24 % годовых. Зная, что проценты мы можем реинвестировать, мы можем посчитать, сколько же мы получим по второму вкладу через год, добавляя каждый месяц проценты к вкладу.

Итак, S = S0 × (1 + 24 % / 12) 12= 1,268 × S0.

Мы видим, что несмотря на кажущуюся более низкую процентную ставку, наш вклад растёт на 26,8 %, что больше первого предложения 25 % годовых.

Поэтому понимание механизма сложных процентов важно и при обычных бытовых финансовых вопросах.

Мы разобрались, как преумножаются деньги, вложенные под процент, и как сравнить два вклада с идентичными сроками действия. Но жизнь, естественно, менее линейна, гораздо чаще в ней встречаются более сложные для сравнения условия.

Так, типичный инвестиционный проект (покупка оборудования, строительство здания, расширение деятельности, другое) выглядит, как правило, так: сегодня инвестируешь в предполагаемые будущие преимущества, в будущем пользуешься ими.