Алексей Лобанов - Энциклопедия финансового риск-менеджмента
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алексей Лобанов - Энциклопедия финансового риск-менеджмента краткое содержание
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).
Энциклопедия финансового риск-менеджмента - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
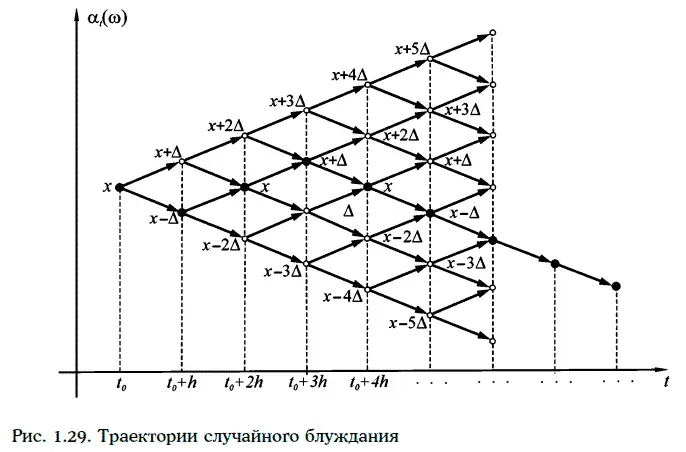
Случайное блуждание α (w, t) обладает независимыми приращениями, причем
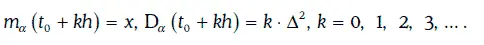
1.27.2. Биномиальная модель
Случайный процесс β(w, t), определенный на множестве
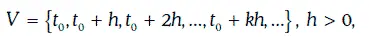
называется биномиальной моделью (binominal model), если
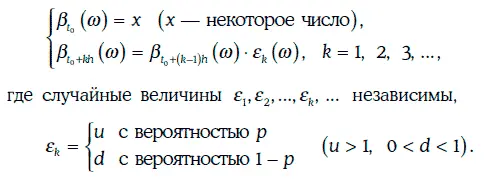
Сечением биномиальной модели в момент времени t 0+ kh является дискретная случайная величина, закон распределения вероятностей которой имеет вид:
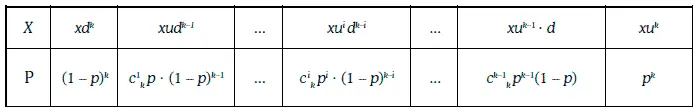
Траектории биноминальной модели изображены на рис. 1.30.
Если случайный процесс β (w, t) является биномиальной моделью с параметрами u, d, p, то
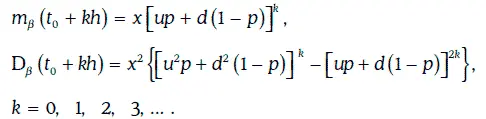
Приращения биномиальной модели, вообще говоря, не являются независимыми. Однако случайный процесс ln β (w, t) имеет независимые приращения.
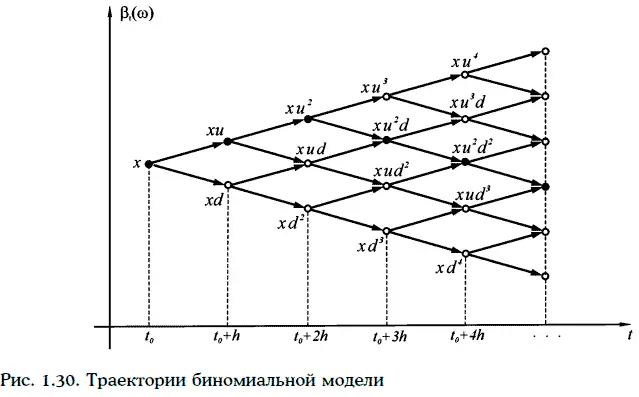
Случайное блуждание и биноминальная модель относятся к случайным процессам с дискретным временем (discrete time process). Важнейшим примером случайного процесса с непрерывным временем (continuous time process) является винеровский случайный процесс.
1.27.3. Винеровский случайный процесс
Случайный процесс w(w, t), определенный на промежутке [t 0, +∞), называется винеровским случайным процессом (Wienerprocess), если выполняются следующие условия:


Для моделирования траекторий винеровского случайного процесса w (w, t) на заданном промежутке времени [t 0, Т] можно применить метод Монте-Карло.
Сам винеровский случайный процесс редко используется для моделирования финансовых показателей, так как имеет постоянное математическое ожидание. Однако на основе винеровского процесса строятся почти все случайные процессы, используемые в настоящее время для моделирования различных финансовых показателей.
1.28. Понятие о стохастических дифференциальных уравнениях
Стохастическим дифференциальным уравнением (stochastic differential equation) называется уравнение вида

Решением стохастического дифференциального уравнения (1.71) на промежутке [t, Т] называется случайный процесс х (w, τ), удовлетворяющий следующим условиям:

Любое решение стохастического дифференциального уравнения (1.71), удовлетворяющее некоторому начальному условию
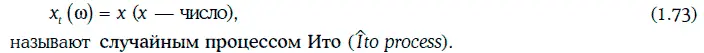
В частности, геометрическим броуновским движением (geometric Brownian motion) является случайный процесс, удовлетворяющий стохастическому дифференциальному уравнению:

Геометрическое броуновское движение, определяемое условиями (1.74) и (1.75), можно найти в явном виде:
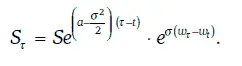

Во многих случаях можно считать, что эволюция цены финансовых активов описывается геометрическим броуновским движением. Такое моделирование оказывается достаточно точным, например, в случае обыкновенных акций.
Пример 1.72.Инвестор считает, что цена бездивидендной акции описывается геометрическим броуновским движением с коэффициентом смещения 0,1 и годовой волатильностью 40 %. В данный момент времени цена акции равна 100 долл. Инвестора интересует цена этой акции через месяц.


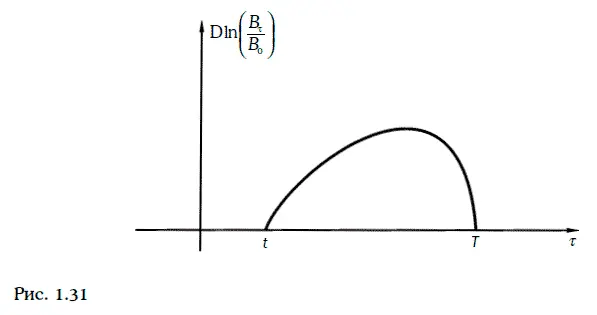
Эволюцию цены В τоблигации с нулевым купоном можно описывать с помощью геометрического броуновского движения, лишь когда до погашения облигации остается достаточно много времени. Действительно, в момент погашения Т ее цена всегда равна номиналу, т. е. известна достоверно. Это означает, что 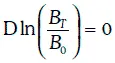 и зависимость
и зависимость 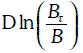 от времени должна иметь вид, изображенный на рис. 1.31.
от времени должна иметь вид, изображенный на рис. 1.31.
Таким образом, при моделировании эволюции цены облигации с нулевым купоном необходимо учитывать эффект приближения к номиналу (pull to par), а геометрическое броуновское движение этот эффект не учитывает, так как 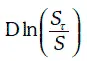 растет во времени линейно.
растет во времени линейно.
В общем случае найти решение стохастического дифференциального уравнения (1.71) в явном виде не удается. Поэтому для моделирования траекторий случайного процесса Ито часто применяется метод Монте-Карло.
Чтобы смоделировать траекторию случайного процесса Ито на отрезке [t, Т], этот отрезок разбивается на n равных частей (n должно быть большим), а затем разыгрывается случайная величина ξ, распределенная нормально с параметрами 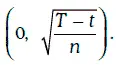 Тогда для последовательности случайных чисел δ 1, δ 2…., δ nбудет построена соответствующая последовательность значений
Тогда для последовательности случайных чисел δ 1, δ 2…., δ nбудет построена соответствующая последовательность значений 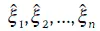 случайной величины ξ, а траектория случайного процесса Ито будет определяться точками:
случайной величины ξ, а траектория случайного процесса Ито будет определяться точками:
Интервал:
Закладка:










