Алексей Лобанов - Энциклопедия финансового риск-менеджмента

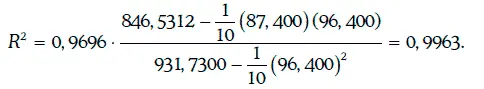
Так как коэффициент детерминации очень близок к единице, то качество регрессионной модели достаточно высокое.

Оценка коэффициентов регрессии получена нами в зависимости от выборки значений X 1, X 2…., X nнезависимой случайной величины ξ и соответствующих им значений зависимой случайной величины η. Для другой выборки значений случайной величины ξ будут получены, вообще говоря, другие оценки коэффициентов регрессии и другая случайная погрешность. В связи с этим возникает задача построения доверительных интервалов для коэффициентов регрессии.

Если предположить, что случайные погрешности не коррелируют между собой (т. е. отсутствует автокорреляция), то доверительные интервалы для коэффициентов регрессии с надежностью 95 % строятся следующим образом:

Если случайная величина ξ принимает значение Х, то согласно линейной регрессионной модели:

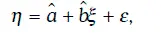
а ожидаемое значение случайной величины η равно

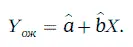
При отсутствии автокорреляции [17] Автокорреляция (autocorrelation, serial correlation) – корреляционная связь между значениями одного и того же случайного процесса в различные моменты времени. и гетероскедастичности [18] Гетероскедастичность (heteroscedasticity) – отсутствие гомоскедастичности, т. е. неоднородность дисперсии, подсчитанной по разным группам (в данном случае – неоднородность дисперсии во времени). доверительный интервал для значения случайной величины η при заданном уровне надежности может быть найден в виде:

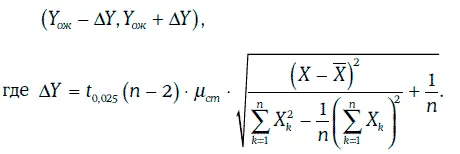
Пример 1.65.Инвестор считает, что через месяц доходность 10-летних казначейских облигаций окажется равной 8 %. Тогда согласно регрессионной модели, построенной в примере 1.63, ожидаемое значение доходности корпоративных облигаций будет равно

Для определения доверительного интервала для доходности корпоративных облигаций с надежностью 95 % найдем:

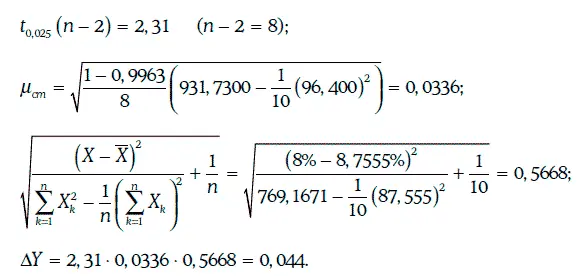
Следовательно, искомый доверительный интервал: (8,87 %; 8,95 %).

Случайная величина γ, принимающая 10 значений: 0, 1, 2, 3, …, 9 с одинаковой вероятностью, называется случайной цифрой.

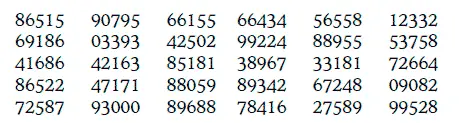
Предположим, что мы произвели N независимых опытов, в результате которых получили N случайных цифр. Записав эти цифры (в порядке их появления) в таблицу, получим то, что называется таблицей случайных цифр. Например, таблица из 150 случайных цифр может иметь следующий вид (цифры разбиты на группы для удобства чтения таблицы):

Случайным числом (random number) называется случайная величина

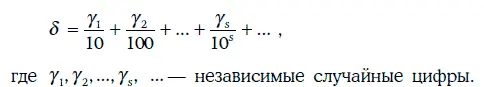
Иными словами, случайное число – это случайная величина, равномерно распределенная на промежутке [0, 1).

Если задана таблица случайных цифр, то можно строить различные случайные числа, как, например:

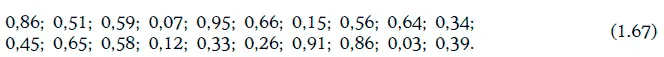
В настоящее время существуют специальные компьютерные программы для построения случайных чисел в любом количестве. Такие программы называют генераторами случайных чисел.

Рассмотрим теперь дискретную случайную величину ξ, распределение которой имеет вид:

Равенство (1.68) позволяет каждому случайному числу приписать определенное значение случайной величине ξ. Такой процесс приписывания значений случайной величине ξ часто называют разыгрыванием этой случайной величины.

Пример 1.66.Случайная величина ξ принимает значения 1 и 2 с вероятностью 0,6 и 0,4 соответственно. В данном случае

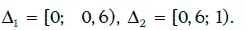
Значения этой случайной величины, приписываемые случайным числом из последовательности (1.67), приведены ниже:

Частоты появления 1 и 2 соответственно равны 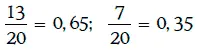и близки к их вероятностям. Чтобы получить лучшую модель, необходимо рассмотреть большее количество случайных чисел.

Предположим, что даны две случайные величины ξ и η, совместное распределение которых имеет вид:

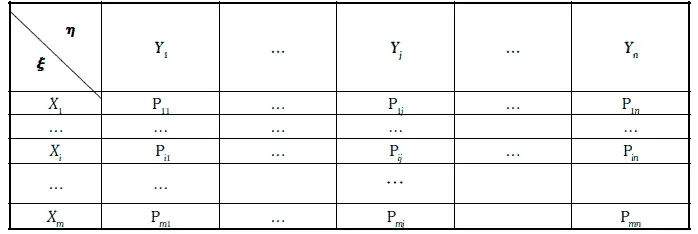
Равенство (1.69) позволяет каждому случайному числу приписать определенную пару значений случайных величин ξ и η. Такой процесс приписывания значений паре случайных величин (ξ, η) называют разыгрыванием этой пары.

Если случайные величины ξ и η независимы, то для разыгрывания пары (ξ, η) достаточно разыграть каждую случайную величину в отдельности. Для разыгрывания непрерывной случайной величины можно вначале найти дискретную случайную величину, близкую к данной случайной величине, а затем разыграть эту дискретную случайную величину.

Метод Монте-Карло позволяет численно находить различные вероятностные характеристики случайной величины η, зависящей от большого числа других случайных величин ξ 1, ξ 2…., ξ n. Этот метод сводится к следующему: разыгрывается последовательность случайных величин (ξ 1, ξ 2…., ξ n), для каждого розыгрыша определяется соответствующее значение случайной величины η, а по найденным значениям строится эмпирическое распределение вероятностей этой случайной величины.