Алексей Лобанов - Энциклопедия финансового риск-менеджмента

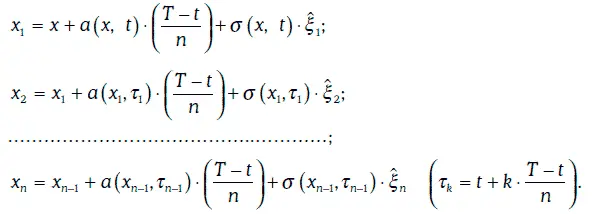
Указанным выше способом можно построить сколь угодно много траекторий случайного процесса Ито.

Дана последовательность независимых одинаково распределенных случайных величин: η 1, η 2…., η n…. с функцией распределения F( x ).

Можно рассмотреть новую последовательность случайных величин {M n}, где M n= max {η 1, η 2…., η n….}, n = 1, 2, 3…..

Функция распределения случайной величины M nопределяется следующим образом:

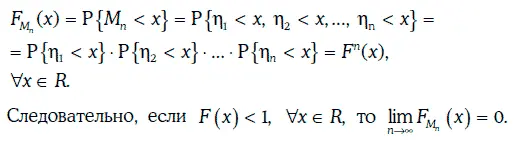
Дана последовательность независимых одинаково распределенных случайных величин η 1, η 2…., η n…..

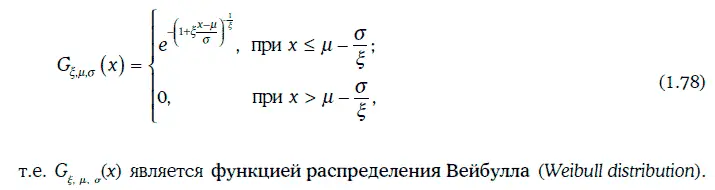
Если случайные величины η 1, η 2, …, η nнезависимы и одинаково распределены, а n достаточно велико, то функция распределения случайной величины M n = max{η 1, η 2, …, η n} практически совпадает с функцией обобщенного распределения экстремальных значений (при подходящем выборе параметров ξ, μ и σ).

Предположим, что случайная величина M n= max{η 1, η 2, …, η n} имеет распределение Фреше, т. е.

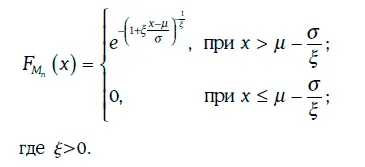
Тогда справедливы следующие утверждения:

1. Плотность распределения случайной величины M nимеет следующий вид (рис. 1.32).

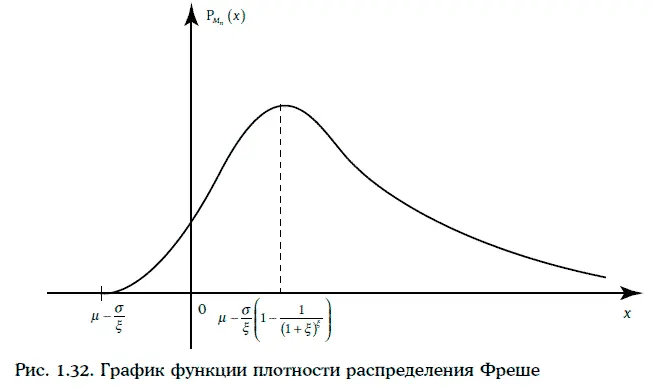
2. Математическое ожидание и дисперсии случайной величины M nможно найти по формулам:

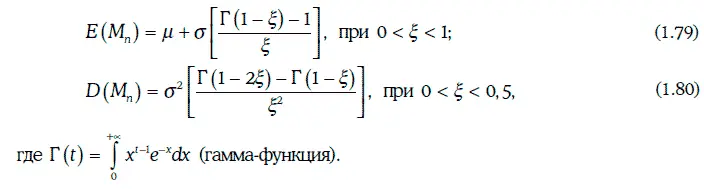
Параметры ξ, μ, σ можно подобрать на основе статистических данных.

Для измерений экстремальных событий может быть использовано распределение Парето (Pareto distribution), которое определяется функцией:

Для большого класса случайных величин η при достаточно большом пороговом значении u справедливо равенство:

Соотношение (1.85) позволяет оценивать «хвосты» распределений на основе статистических данных.

1. Барбаумов В. Е., Гладких И. М., Чуйко А. С. Финансовые инвестиции: Учебник. – М.: Финансы и статистика, 2003.

2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2001.

3. Дуглас Л. Г. Анализ рисков операций с облигациями на рынке ценных бумаг. – М.: Филинъ, 1998.

4. Количественные методы финансового анализа / Под. ред. С. Дж. Брауна, М. П. Крицмена. – М.: ИНФРА-М, 1996.

5. Fabozzi F. J. Fixed income mathematics. 3rd ed. – N.Y.: McGraw-Hill, 1997.

6. Fabozzi F. J. (ed.) Advances in fixed income valuation, modeling and risk management. – Pennsylvania: Associates New Hope, 1997.

В настоящее время для идентификации и измерения рисков широко используется теория производных финансовых инструментов. Изучение производных финансовых инструментов важно еще и потому, что сами эти инструменты являются источниками рисков как для различных финансовых институтов, так и для финансового рынка в целом. Кроме того, производные финансовые инструменты – одно из важнейших средств хеджирования тех или иных рисков. Именно поэтому данная глава посвящена изучению производных финансовых инструментов.

В главе рассматриваются как простейшие производные финансовые инструменты – форвардные и фьючерсные контракты, свопы, так и более сложные – опционы различных видов и инструменты со встроенными опционами. Основное внимание уделяется методам оценки таких инструментов и основным направлениям их использования.

Важнейшими производными финансовыми инструментами являются классические европейские и американские опционы. Подробно рассматриваются методы оценки таких опционов в случае, когда стоимость исходных активов определяется геометрическим броуновским движением. В частности, приводятся формулы Блэка-Шоулза для оценки европейских опционов и разбирается их использование. Применение классических опционов для хеджирования основных финансовых рисков также рассматривается в данной главе.

В заключительной части главы обосновывается построение биномиальной модели процентной ставки и ее использование для оценки финансовых инструментов, производных от процентных ставок: кэпов, флоров, свопционов и облигаций со встроенными опционами. Кроме того, приводится обзор и других моделей временной структуры процентных ставок.

В настоящее время на развитых финансовых рынках важную роль играют так называемые производные инструменты (derivatives). Простейшим из производных инструментов является форвардный контракт.

Форвардный контракт, или форвард (forward), представляет собой соглашение купить или продать некоторые активы, называемые «базисными» (underlying), в определенный момент времени в будущем по заранее установленной цене. Обычно форвардные контракты заключаются между финансовым институтом и одним из его корпоративных клиентов. Таким образом, в форвардном контракте всегда присутствуют две стороны. При этом говорят, что сторона, согласившаяся в будущем купить активы, занимает длинную позицию, а сторона, согласившаяся продать активы, – короткую.

Так как стороны форвардного контракта равноправны и подвержены одному и тому же риску, то при заключении форвардного контракта никто никому ничего не платит. Это означает, что в момент заключения форвардного контракта стоимость его равна нулю.

Цену, по которой стороны согласились купить (и соответственно продать) активы, называют ценой поставки активов (delivery price). Цену поставки обозначим через K. Момент времени, когда происходит покупка и продажа активов, называют датой исполнения форвардного контракта, или датой поставки. Момент исполнения форвардного контракта обозначим через Т.