Алексей Лобанов - Энциклопедия финансового риск-менеджмента

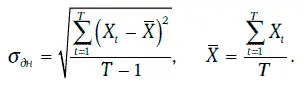
Иными словами, дневная волатильность принимается равной стандартному отклонению логарифма относительного изменения финансового показателя за один день.

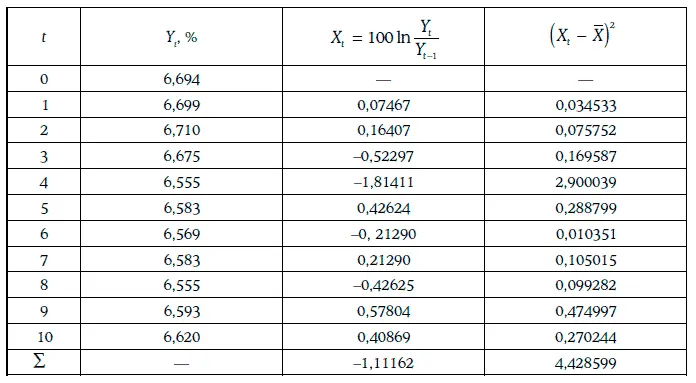
Пример 1.60.В течение 11 последовательных рабочих дней биржи определялась доходность 30-летних казначейских облигаций с нулевыми купонами. Расчет дневной волатильности доходности на основе этой информации приведен ниже.

Таким образом, дневная волатильность доходности 30-летних облигаций с нулевыми купонами оценивается в 0,70 %.

Если случайные величины X tне коррелируют между собой, то, зная дневную волатильность доходности финансового инструмента, можно оценить волатильность доходности этого инструмента за данный период времени:

В частности, для того чтобы определить годовую волатильность, необходимо для каждого конкретного случая правильно определить число рабочих дней в году. Число рабочих дней в году может быть равным 250, 260 или 365.

Пример 1.61.В примере 1.60 была найдена дневная волатильность доходности 30-летних казначейских облигаций с нулевыми купонами: σ дн = 0,70147.

Ниже указана годовая волатильность доходности при разных оценках числа дней в году:

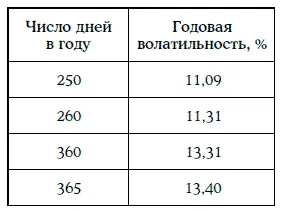
Предположим, что в данный момент времени доходность финансового инструмента равна r. Можно считать, что доходности за один день распределены логнормально с параметрами 0 и σ дн . Если логарифмы относительных изменений доходности не коррелируют между собой, то отношение доходности через год к доходности г будет распределено также логнормально, но с параметрами (0, σ год ). Следовательно, сама доходность финансового инструмента через год должна иметь логнормальное распределение с параметрами (ln r, σ год ).

Если годовая волатильность доходности достаточно мала, то можно считать, что доходность финансового инструмента через год распределена приблизительно нормально с параметрами r и rσ год .

Пример 1.62.Текущая доходность 10-летних казначейских облигаций с нулевым купоном равна 8 %, а годовая волатильность этой доходности равна 15 %.

Можно предположить, что доходность 10-летних облигаций с нулевыми купонами через год будет приблизительно распределена нормально с ожидаемым значением 0,08 и стандартным отклонением 0,08-0,15 = 0,012. Отсюда, в частности, следует, что с вероятностью 95,5 % доходность через год окажется между 0,08-2 • 0,012 = 0,056 и 0,08 + 2 • 0,012 = 0,104, т. е. будет принимать значение между 5,60 и 10,40 %.

Во многих случаях требуется установить зависимость между двумя случайными величинами. Чаще всего предполагается линейная зависимость. Например, при обмене облигаций использовалась линейная зависимость между изменениями доходностей двух облигаций.

Рассмотрим две случайные величины ξ и η и предположим, что когда случайная величина ξ принимает значения X 1, X 2…., X n, то случайная величина η принимает соответственно значения Y 1, Y 2…., Y n.

Линейной регрессионной моделью называют уравнение следующего вида:

При построении линейной регрессионной модели коэффициенты а и b необходимо подобрать так, чтобы влияние случайной погрешности ξ на случайную величину η было как можно меньше.

Из уравнения (1.64) следует, в частности, что

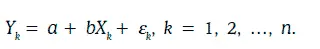
Коэффициенты регрессии а и b чаще всего подбираются методом наименьших квадратов (least squares), который сводится к отысканию значений а и b так, чтобы достигалось наименьшее значение функции

Нетрудно проверить, что наименьшее значение функции (1.65) достигается при

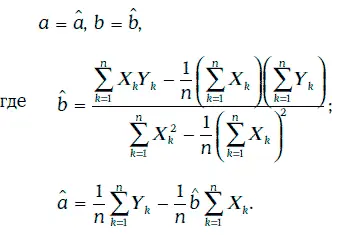
При выборе коэффициентов регрессии указанным выше способом будут выполняться следующие соотношения:

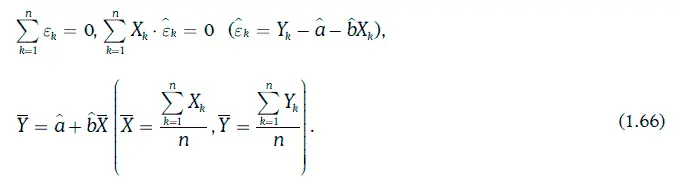
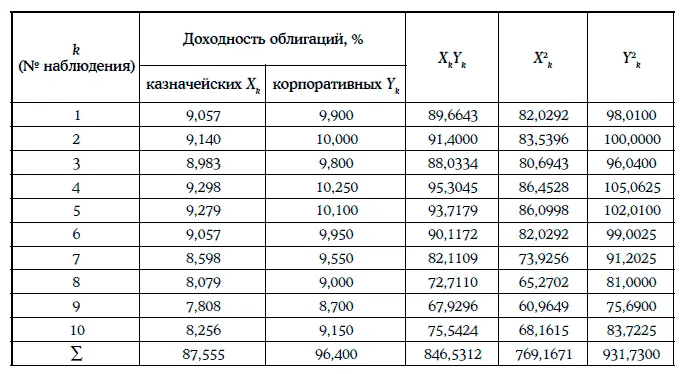
Пример 1.63.Построение линейной регрессионной зависимости доходности среднесрочных корпоративных облигаций одного и того же кредитного рейтинга (η) от доходности 10-летних казначейских облигаций (ξ). Исходная информация и предварительные расчеты приведены в таблице ниже.

Коэффициенты регрессии находят следующим образом:

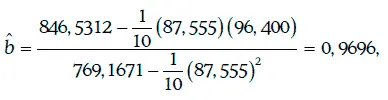
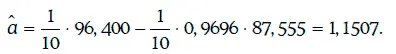
Уравнение регрессии в данном случае имеет вид:

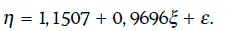
Из соотношения (1.66) следует, что

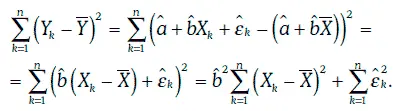
Отношение суммы квадратов, объясняемой регрессией, к полной сумме квадратов называют коэффициентом детерминации и обозначают R 2. Таким образом,

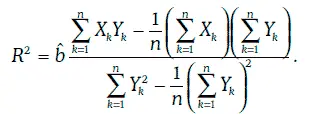
Коэффициент детерминации всегда находится между 0 и 1, причем чем ближе коэффициент детерминации к единице, тем выше качество регрессионной модели.

Пример 1.64.Оценим качество регрессионной модели, построенной в примере 1.63.

В данном случае коэффициент детерминации может быть найден следующим образом: