Алексей Лобанов - Энциклопедия финансового риск-менеджмента

где F ξ(x) – функция распределения вероятностей случайной величины ξ.

Функция p ξ(x), удовлетворяющая условию (1.50), называется плотностью распределения вероятностей (probability density function – PDF) случайной величины ξ.

Равенство (1.50) означает, что заштрихованная площадь на рис. 1.18 под графиком плотности распределения равна вероятности того, что случайная величина принимает значение меньше х.

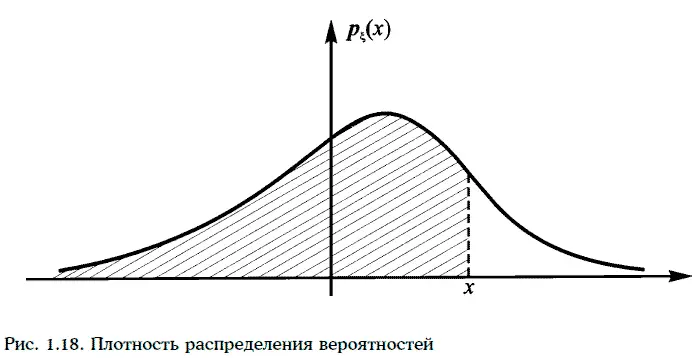
1. Вероятность того, что непрерывная случайная величина принимает значение между х 1и x 2(x 1< x 2), совпадает с заштрихованной площадью на рис. 1.19.

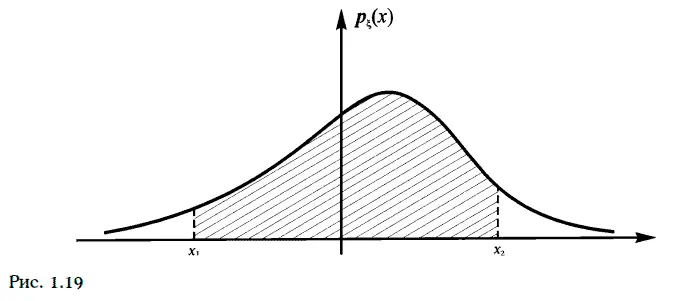
2. Если p ξ(x) – плотность распределения вероятностей случайной величины, то

3. Вероятность того, что непрерывная случайная величина ξ принимает то или иное значение, всегда равна нулю, т. е. P{ξ = x} = 0.

4. Производная функции распределения вероятностей непрерывной случайной величины равна плотности распределения вероятностей этой случайной величины, т. е.

Математическое ожидание и дисперсия непрерывной случайной величины ξ могут быть найдены следующим образом:

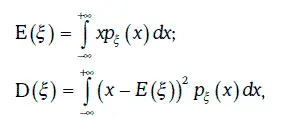
где P ξ(x) – плотность распределения вероятностей случайной величины ξ. Стандартное отклонение случайной величины определяется обычно как:

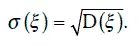
Если f(t) – некоторая непрерывная функция, а ξ – непрерывная случайная величина, то

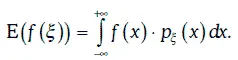
Пример 1.50.Случайная величина ξ равномерно распределена на отрезке [a, b], если

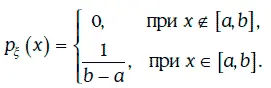
Функцию распределения случайной величины ξ можно найти следующим образом:

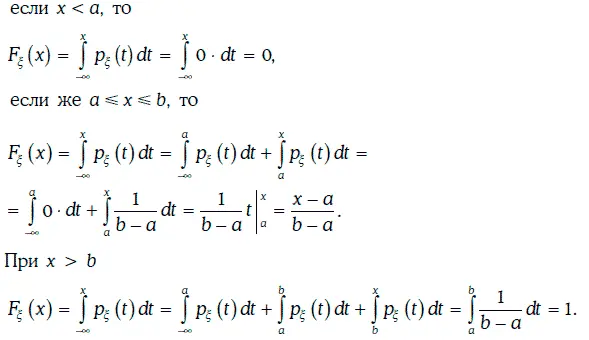
Таким образом,

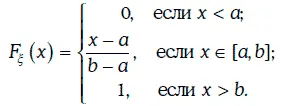
Математическое ожидание и дисперсию случайной величины ξ можно найти следующим образом:

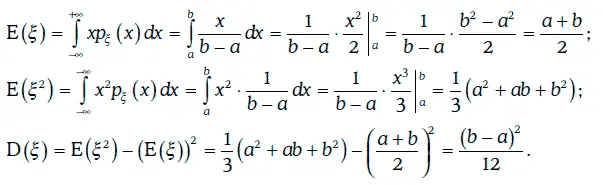
Пример 1.51.Случайная величина ξ распределена показательно, если

Асимметрией (skewness) распределения вероятностей случайной величины ξ называется число

Если a (ξ) = 0, то плотность распределения вероятностей случайной величины ξ симметрична относительно математического ожидания этой случайной величины (рис. 1.20).

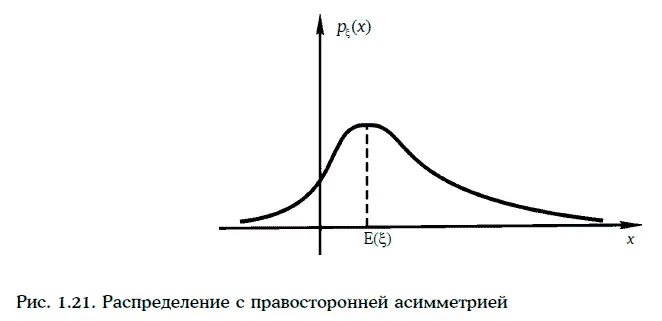
При положительной (правосторонней) асимметрии распределения правая ветвь (tail) плотности распределения вероятностей случайной величины «длиннее» левой ветви. Соответственно, при отрицательной (левосторонней) асимметрии правая ветвь плотности распределения вероятностей случайной величины будет «короче» левой ветви (рис. 1.21 и 1.22).

Эксцессом(kurtosis) распределения вероятностей случайной величины ξ называется число

При одном и том же стандартном отклонении чем больше эксцесс, тем «тяжелее» ветви плотности распределения вероятностей случайной величины (рис. 1.23).

Распределение вероятностей с большим эксцессом называют распределением с «тяжелыми» ветвями (leptokurtic/fat-tailed distribution).

Медианой (median) распределения случайной величины ξ называется число Ме, удовлетворяющее условию:

Модой (mode) распределения случайной величины ξ называется любая точка локального максимума плотности распределения P ξ(x) этой случайной величины.

Распределение с одной модой Мо называется унимодальным (unimodal).

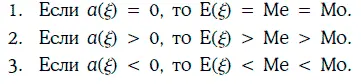
Если даны две случайные величины ξ 1и ξ 2, то можно рассмотреть двумерную случайную величину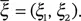

Функция Pξ(x 1, x 2), удовлетворяющая равенству (1.54), называется плотностью совместного распределения случайных величин ξ 1и ξ 2.

Все основные свойства числовых характеристик, рассмотренные нами для дискретных случайных величин, сохраняются и в непрерывном случае.