Алексей Лобанов - Энциклопедия финансового риск-менеджмента
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алексей Лобанов - Энциклопедия финансового риск-менеджмента краткое содержание
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).
Энциклопедия финансового риск-менеджмента - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:


Пример 1.46.Бросаются две одинаковые игральные кости. В данном случае элементарное событие характеризуется следующей парой чисел: числом, выпавшим на первой кости, и числом, выпавшим на второй кости, а пространство элементарных событий состоит из 36 событий:




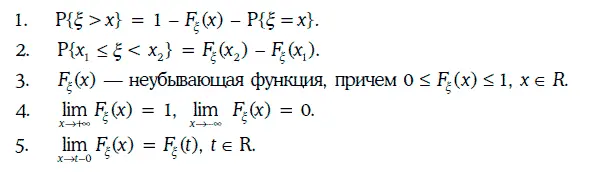

1.20. Дискретные случайные величины
Случайная величина ξ называется дискретной случайной величиной (discrete random variable), если она принимает лишь конечное или счетное число различных значений.
Чтобы задать дискретную случайную величину, достаточно указать закон распределения вероятностей этой случайной величины в следующем виде:
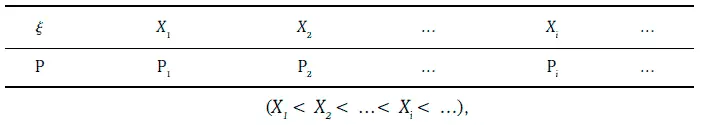
т. е. для каждого возможного значения случайной величины ξ задать вероятность этого значения.

Функция распределения вероятностей дискретной случайной величины ξ показана на рис. 1.17.
Основные числовые характеристики дискретной случайной величины ξ определяются следующим образом:

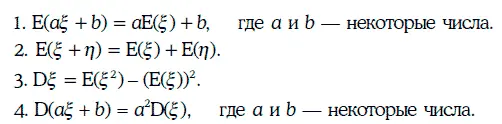
Пример 1.48.Дана 10 %-ная облигация с полугодовыми купонами, продающаяся по номиналу, когда до ее погашения остается 20,5 года. Инвестор считает, что доходность к погашению этой облигации через 6 месяцев может принять следующие значения:

Законы распределения вероятностей цены облигации (η) и годовой реализуемой доходности за 6 месяцев (τ) указаны в таблице:
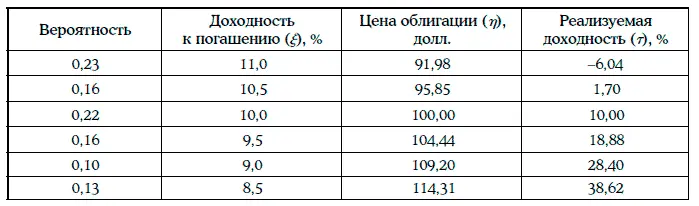
Например, если ξ = 11,0 %, то
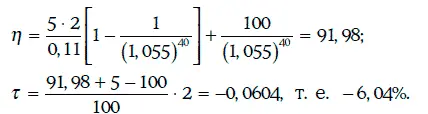
Математическое ожидание цены облигации через 6 месяцев и ее дисперсия могут быть найдены следующим образом:

Таким образом, ожидаемое значение реализуемой доходности облигации за 6 месяцев равно 11,96 %, а ее стандартное отклонение составляет 14,81 %.
Закон совместного распределения вероятностей двух случайных величин ξ и η может быть задан следующим образом:
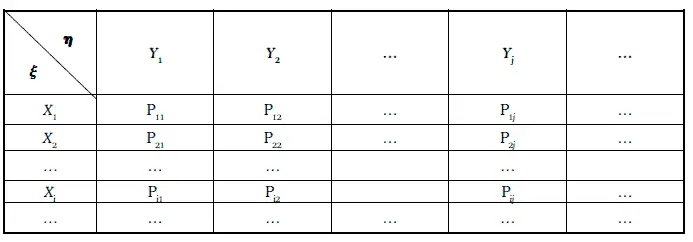
P ij – это вероятность того, что случайная величина ξ принимает значение X i, а случайная величина η – значение Y j, i = 1, 2, 3…, j = 1, 2, 3…, причем
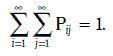
Зная закон совместного распределения вероятностей двух случайных величин, можно найти закон распределения вероятностей каждой из этих случайных величин, так как
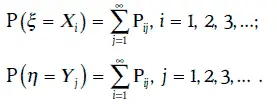
Дискретные случайные величины ξ и η называются независимыми, если
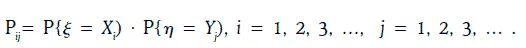
Для независимых случайных величин справедливы следующие два равенства:
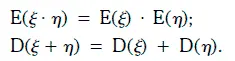
Ковариация (covariance) между двумя дискретными случайными величинами ξ и η определяется равенством
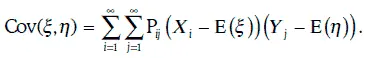
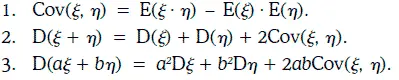
Корреляция (correlation) между двумя случайными величинами ξ и η определяется следующим образом:
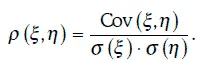
Случайные величины называются некоррелированными, если корреляция между ними равна 0.

Пример 1.49. Совместное распределение вероятностей случайных величин ξ и η приведено в таблице:
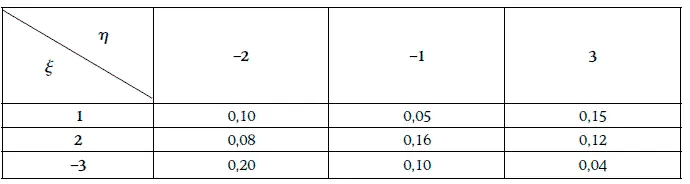
Распределение вероятностей случайных величин ξ,η и ξη имеет следующий вид:
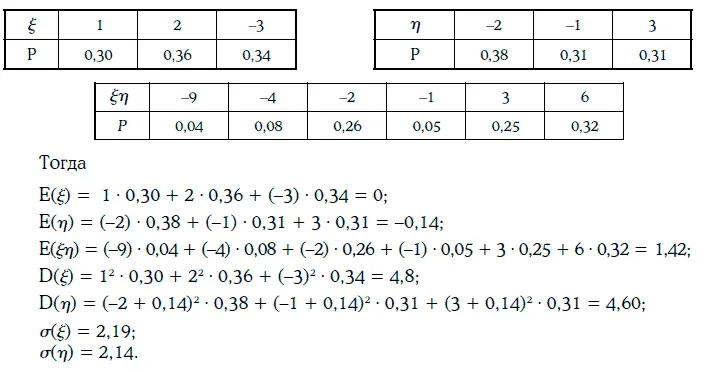
Ковариация и корреляция между случайными величинами ξ и η находятся следующим образом:

1.21. Непрерывные случайные величины
Случайная величина ξ называется [абсолютно] непрерывной (continuous random variable), если существует неотрицательная функция p ξ(x), такая, что
Читать дальшеИнтервал:
Закладка:










