Алексей Лобанов - Энциклопедия финансового риск-менеджмента

Модифицированная дюрация и выпуклость портфеля А находятся следующим образом:

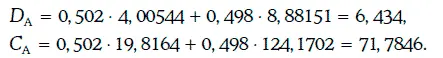
Таким образом, дюрации портфелей А и В одинаковы, а выпуклость портфеля А выше выпуклости портфеля В.

Относительные изменения стоимостей портфелей А и В при различных изменениях требуемых доходностей облигаций на одну и ту же величину приведены в следующей таблице:

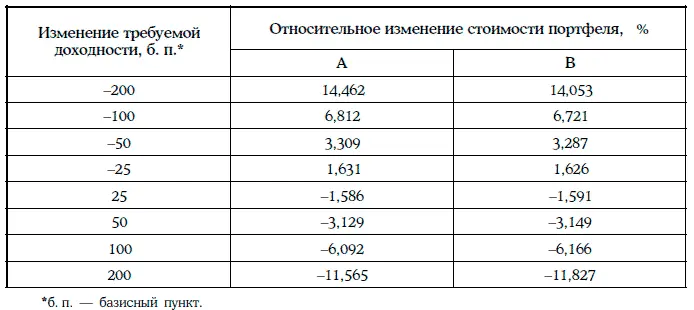
Таким образом, при различных параллельных сдвигах кривой доходностей относительное изменение стоимости портфеля А всегда больше относительного изменения стоимости портфеля В.

При непараллельных сдвигах кривой доходностей (yield curve twist), т. е. когда требуемые доходности изменяются по-разному, ситуация может оказаться противоположной. В частности, если требуемые доходности облигаций Х, Y и Z уменьшаются на 75, 25 и 50 б. п. соответственно, то относительные изменения стоимостей портфелей А и В будут равны 2,662 и 3,287 %, т. е. относительный рост стоимости портфеля А окажется ниже относительного роста стоимости портфеля В.

Основные характеристики портфеля облигаций – средневзвешенная (или внутренняя) доходность, модифицированная дюрация и выпуклость – используются для сравнения портфеля облигаций с точки зрения их инвестиционного качества.

Однако эти характеристики не всегда дают возможность сделать правильный вывод.

Пример 1.44[5]. Рассмотрим портфели А и В из предыдущего примера 1.43. Основные характеристики этих портфелей приведены в таблице:

Для сравнения портфелей А и В воспользуемся показателем, называемым годовой реализуемой доходностью за 6 месяцев.

В данном случае годовая реализуемая доходность за 6 месяцев портфелей А и В может быть найдена по формуле:

В таблице показаны разности годовых реализованных доходностей портфелей А и В (R B – R A) при различных сдвигах кривой доходностей:

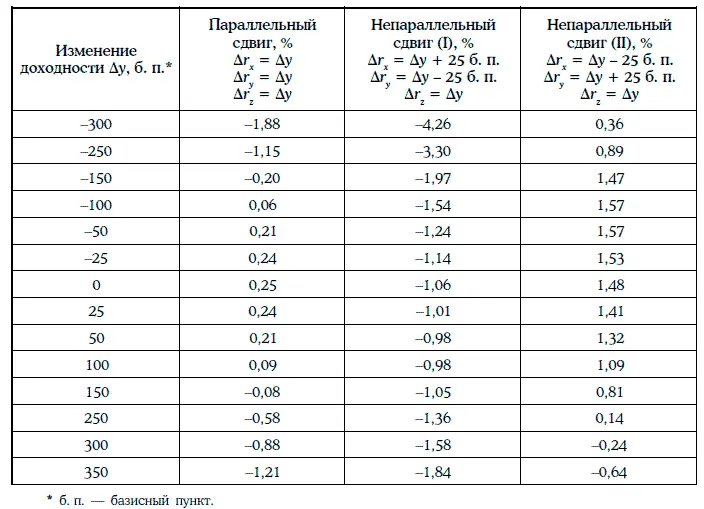
Таким образом, инвестиционная эффективность не определяется основными характеристиками портфелей А и В, а зависит от того, какие изменения требуемых доходностей происходят на рынке.

Множество(set) – это совокупность некоторых объектов. Объекты, из которых состоит множество А, называют элементами этого множества.

Если а является элементом множества А, то пишут а ∈ А.

Задать множество можно, либо перечислив все его элементы, либо указав характеристическое свойство, которому должны удовлетворять все элементы этого множества.

Например, запись А = { a 1, a 2, a 3, a 4} означает, что множество А состоит из элементов a 1, a 2, a 3, a 4.

Множество В всех действительных чисел, удовлетворяющих неравенству х 2 – 2х + 3 ≤ 0, можно записать следующим образом:

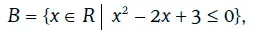
где R – множество всех действительных чисел.

Множество А называют подмножеством (subset) множества В, если каждый элемент множества А является элементом множества В (рис. 1.13).

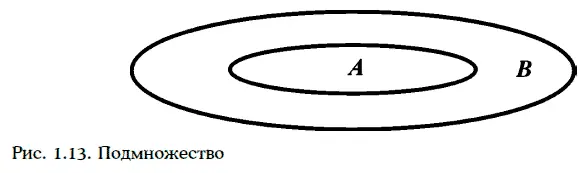
Если множество А является подмножеством множества В, то пишут А ⊂ В. Например, множество А = {1, 2, 3} является подмножеством множества В = {1, 2, 3, 4, 5}. Множество Z всех целых чисел является подмножеством множества R всех действительных чисел.

Разностью А\В двух множеств А и В называют множество всех элементов А, не попавших в множество В (рис. 1.14).

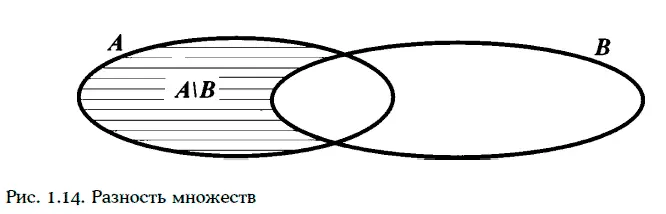
Если В ⊂ А, то разность А\В называют дополнением множества В до множества А. Например, если А = {1, 2, 3, 4}, а В = {3, 4, 5, 6}, то А\В = = {1, 2}.

Пересечением двух множеств А и В называют множество, обозначаемое А ∩ B, все элементы которого принадлежат как множеству А, так и множеству В (рис. 1.15).

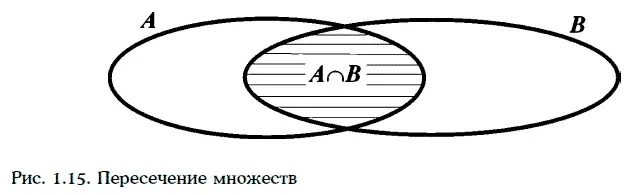
Например, если А = {1, 2, 3}, а В = {1, 3, 4, 5}, то А ∩ В = {1, 3}.

Если множества А и В не содержат общих элементов, то говорят, что они не пересекаются, и пишут A ∩ B = ∅ (∅ – символ пустого множества).

Аналогично можно определить пересечение трех, четырех и более множеств. В частности, множество 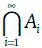является совокупностью всех элементов, принадлежащих каждому из множеств А 1, А 2…., А i…..

Объединением двух множеств А и В называют множество, обозначаемое А ∪ B, все элементы которого принадлежат хотя бы одному из множеств А и В (рис. 1.16).

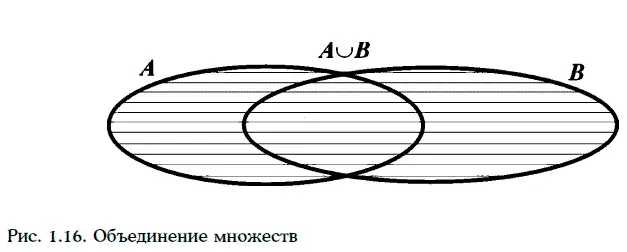
Например, если А = {1, 2, 3, 4}, а В = {3, 4, 5, 6}, то А ∪ В = {1, 2, 3, 4, 5, 6}. Точно так же определяется объединение трех, четырех и более множеств. В частности, множество 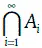– это совокупность всех элементов, принадлежащих хотя бы одному из множеств А 1, А 2…., А i…..

Пусть Ω – некоторое множество. В дальнейшем элементы множества Ω будем называть элементарными событиями, а само множество Ω – пространством элементарных событий.

Набор β подмножеств множества Ω называется σ-алгеброй случайных событий при выполнении следующих трех условий:

Если пространство элементарных событий конечно, т. е. состоит из конечного числа элементарных событий, то в качестве σ-алгебры случайных событий обычно рассматривают набор всех подмножеств этого пространства.

Пример 1.45.Бросается игральная кость. Пространство элементарных событий состоит из 6 событий: выпадение любого целого числа от 1 до 6. Выпадение четного числа является случайным событием, так как состоит из трех элементарных событий: выпадение чисел 2, 4 или 6. Выпадение числа, меньшего 3, также является случайным событием.

Говорят, что на σ-алгебре случайных событий β определена вероятностная мера Р, если каждому случайному событию A ∈ β поставлено в соответствие неотрицательное число Р(А) так, что выполняются следующие условия: