Алексей Лобанов - Энциклопедия финансового риск-менеджмента

Если же инвестор взял облигацию взаймы у дилера и продал ее на рынке, то говорят, что на рынке облигаций он занимает короткую позицию (short position). Инвестор, занимающий короткую позицию, обязан в определенный момент времени в будущем вернуть облигацию дилеру и выплатить компенсацию за недополученные купонные платежи. Рассмотрим на примере, как определить модифицированную дюрацию портфеля, состоящего из длинных и коротких позиций на рынке облигаций.

Пример 1.38.Портфель состоит из двух позиций: длинной позиции в размере 100 млн долл. по двухлетней облигации ценой 101 долл. с модифицированной дюрацией 1,7 и короткой позиции в размере 50 млн долл. по 5-летней облигации ценой 99 долл. с модифицированной дюрацией 4,1. Определим модифицированную дюрацию этого портфеля.

Исходная стоимость портфеля может быть найдена следующим образом:

Предположим, что инвестор рассматривает вопрос об обмене облигации Х стоимостью V Xс модифицированной дюрацией 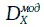на облигацию Y с модифицированной дюрацией 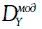при цене P Y (на номинал 100 долл.).

Выясним, каким должен быть номинал облигации Y, чтобы обмен облигации Х на облигацию Y не увеличивал подверженность инвестора процентному риску.

Если требуемая доходность облигации Х изменится на величину Δr, то соответствующее изменение стоимости этой облигации определяется равенством

Можно предположить, что на основе статистических исследований установлено, что при изменении требуемой доходности облигации Х на величину Δr требуемая доходность облигации Y изменяется на величину βΔr.

Тогда соответствующее изменение стоимости облигации Y можно найти по формуле:

где A y – номинал облигации Y.

Обмен облигаций не будет увеличивать подверженность процентному риску, если при любом Δr

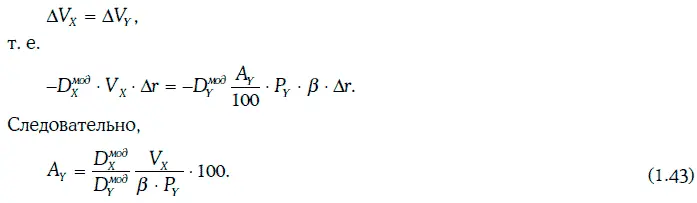
Равенство (1.43) показывает, каким должен быть номинал облигации Y, чтобы при обмене облигации Х на облигацию Y не увеличивался процентный риск.

Пример 1.39.Инвестор рассматривает вопрос об обмене облигации Х стоимостью 8 млн долл. на облигацию Y при цене P Y= 96 долл. Модифицированные дюрации облигаций Х и Y равны 5 и 4 соответственно, а коэффициент β равен 1,6.

Чтобы при обмене не менялась подверженность процентному риску, номинал облигации Y должен удовлетворять равенству:

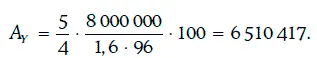
Таким образом, искомый номинал облигаций Y должен равняться 6 510 417.

Предположим, что в данный (нулевой) момент времени инвестор владеет портфелем облигаций, который он собирается продать через Т лет.

Если в данный момент времени все рыночные доходности одинаковы, т. е. кривая доходности имеет ровный вид, то будущая стоимость инвестиций П А(Т) через Т лет определяется следующим образом:

где r – рыночная доходность,

П(r) – стоимость портфеля при рыночной доходности, равной r.

Будущую стоимость П А(Т) будем называть целевой накопленной стоимостью портфеля облигаций.

Однако если между данным моментом времени и первым процентным платежом рыночные доходности изменяются на одну и ту же величину Δr, а в дальнейшем уже меняться не будут, то будущая стоимость инвестиции П ф(Т) через Т лет удовлетворяет равенству

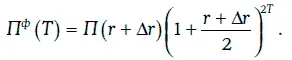
Будущую стоимость П ф(Т) будем называть фактической накопленной стоимостью портфеля облигаций.

Фактическая накопленная стоимость портфеля облигаций может оказаться выше или ниже целевой накопленной стоимости этого портфеля. Однако если временной горизонт инвестора Т совпадает с дюрацией Маколея портфеля облигаций, то фактическая накопленная стоимость портфеля никогда не будет меньше его целевой накопленной стоимости.

Пример 1.40.Рассмотрим портфель из двух облигаций с полугодовыми купонами, когда все рыночные доходности равны 6 %. Основные данные об облигациях портфеля приведены ниже в таблице:

Дюрация Маколея данного портфеля облигаций находится следующим образом:

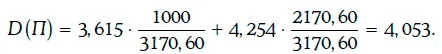
Целевая накопленная стоимость портфеля через 4,053 года будет равна:

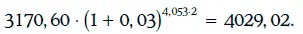
В таблице указаны фактические накопленные стоимости через 4,053 года при различных изменениях рыночных доходностей:

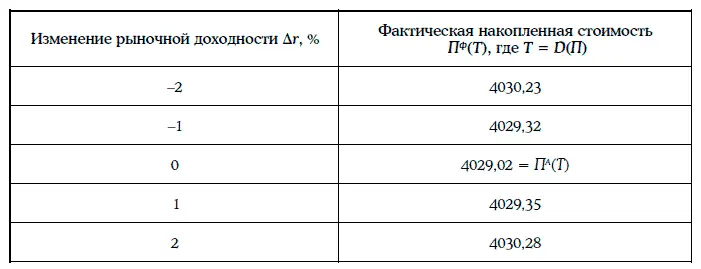
Стратегия иммунизации портфеля облигаций рассчитана на защиту портфеля облигаций от процентного риска. Эта стратегия предполагает следующие действия. В начальный момент времени формируется портфель облигаций так, чтобы дюрация Маколея этого портфеля совпадала с временным горизонтом инвестора. С годами портфель периодически пересматривается так, чтобы каждый раз дюрация Маколея совпадала с временным горизонтом инвестора.

Рассмотрим финансовый инструмент со следующим потоком платежей:

Если требуемая доходность при начислении процентов дважды в год равна r, то выпуклостью (convexity) данного финансового инструмента называют число

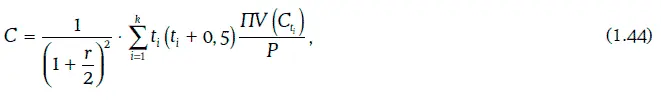
Имеет место следующее равенство: