Алексей Лобанов - Энциклопедия финансового риск-менеджмента

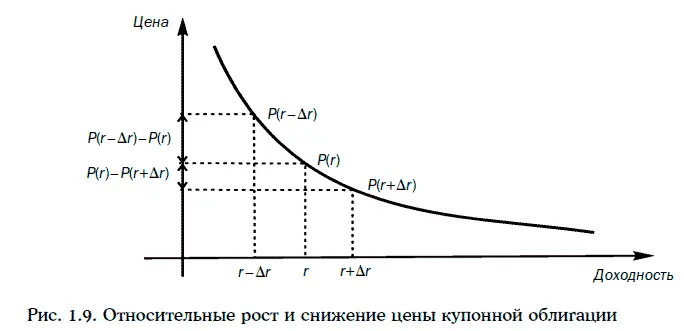
Пример 1.28.Дана 8 %-ная купонная облигация с полугодовыми купонами, до погашения которой остается 15 лет, когда требуемая доходность равна 10 %, а цена облигации – 84,6275 долл.

Относительный рост и относительное снижение цены облигации при различных изменениях требуемой доходности приведены в таблице:

Замечание . При достаточно малых изменениях требуемой доходности относительный рост цены облигации практически совпадает с относительным снижением.

2. Чем выше купонная ставка облигации, тем меньше относительное изменение цены купонной облигации.

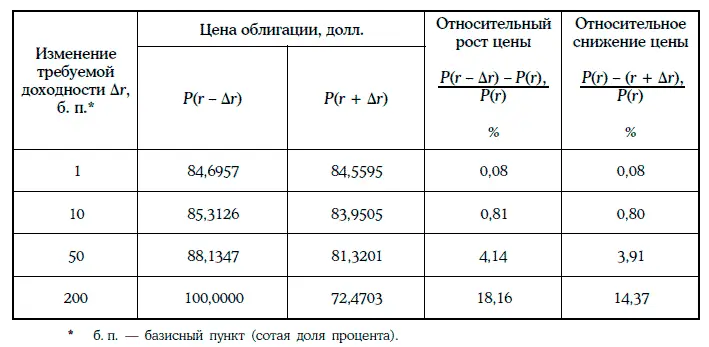
Пример 1.29.Даны 5-летние облигации с полугодовыми купонами при требуемой доходности r = 10 %, купонные ставки которых равны 0, 8 и 12 %. Относительный рост и относительное снижение цен облигаций при изменении требуемой доходности на 10 базисных пунктов приведены в таблице:

Следствие . Среди облигаций с одним и тем же сроком до погашения, выпущенных данным эмитентом, наиболее рискованными являются облигации с нулевым купоном.

3. Чем выше требуемая доходность при прочих равных условиях, тем ниже относительное изменение цены купонной облигации.

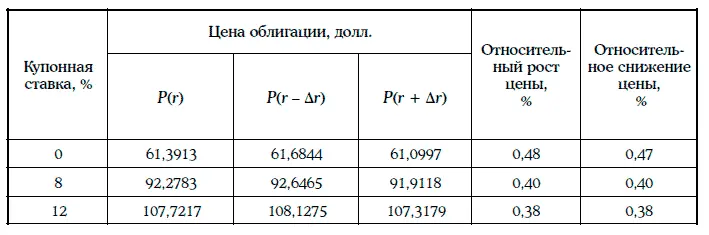
Пример 1.30.Дана 8 %-ная купонная облигация с полугодовыми купонами, до погашения которой остается 15 лет, когда требуемая доходность равна 12 %, а цена облигации равна 72,4703 долл.

Относительный рост и относительное снижение цены облигации при различных изменениях требуемой доходности, приведенные в таблице, сравним с аналогичными показателями для облигации из примера 1.28:

4. Чем меньше времени остается до погашения облигации, тем меньше относительное изменение цены облигации (за исключением долгосрочных облигаций, продающихся с дисконтом).

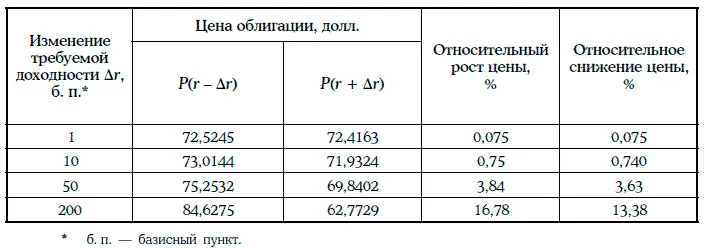
Пример 1.31.Рассмотрим 4 %-ную облигацию с полугодовыми купонами при разных сроках погашения, если требуемая доходность равна 10 %, а изменение требуемой доходности составляет 50 базисных пунктов.

Все расчеты приведены в таблице:

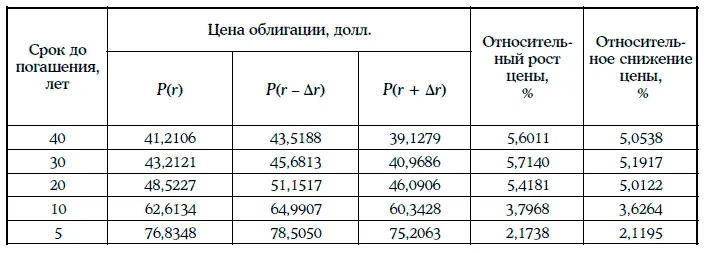
Следствие . Если ожидается падение процентных ставок на рынке, то следует держать долгосрочные облигации, а если ожидается рост процентных ставок, то краткосрочные.

Для оценки рискованности облигаций используется показатель, называемый ценой базисного пункта.

Ценой базисного пункта (price value of a basis point – PVBP) называют изменение цены облигации номиналом 100 долл. при уменьшении требуемой доходности на один базисный пункт.

Таким образом, цена базисного пункта определяется следующей формулой:

где δP – цена базисного пункта облигации;

Р(r) – цена облигации номиналом 100 долл. при требуемой доходности, равной r;

Р(r – Δr) – цена облигации при требуемой доходности, равной r – Δr;

Δr = 0,0001.

Замечание

1. Изменение цены облигации номиналом 100 долл. при увеличении требуемой доходности на 1 базисный пункт практически совпадает с ценой базисного пункта этой облигации.

2. Изменение цены облигации номиналом 100 долл. при уменьшении (увеличении) требуемой доходности на х базисных пунктов при х ≤ 10 приблизительно равно произведению цены базисного пункта на число х .

Пример 1.32.Рассмотрим 6 %-ную облигацию с полугодовыми купонами, когда до погашения остается 10 лет, а требуемая доходность равна 10 %.

В данном случае

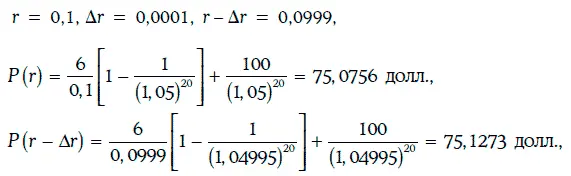
и по формуле (1.30) цена базисного пункта

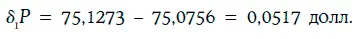
Следовательно, изменение цены облигации при увеличении требуемой доходности на 8 базисных пунктов должно приблизительно равняться:

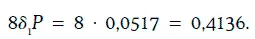
Точное значение этого изменения может быть найдено следующим образом:

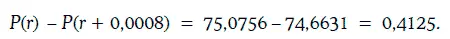
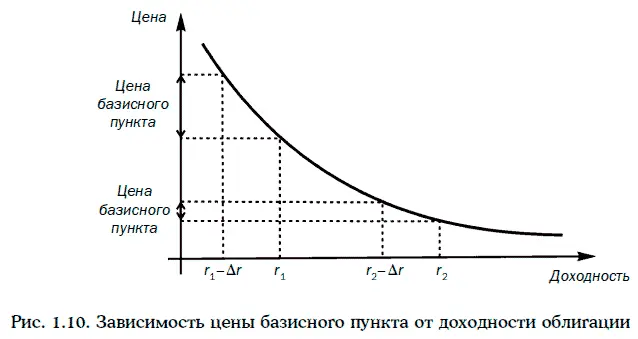
Нетрудно проверить, что имеет место следующее утверждение: чем выше требуемая доходность для данной облигации, тем ниже цена базисного пункта (рис. 1.10).

Пример 1.33.Рассмотрим облигацию из примера 1.32 при требуемой доходности 6 %. В этом случае цена базисного пункта

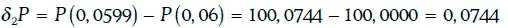
превышает цену базисного пункта из примера 1.32.

Цена базисного пункта для портфеля облигаций находится по формуле:

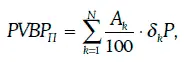
где A k – номинальная стоимость облигации k-го вида

δ kP – цена базисного пункта облигации k-го вида при номинале 100 долл.;

N – число облигаций в портфеле.

Рассмотрим финансовый инструмент со следующим потоком платежей:

Если требуемая доходность при начислении процентов дважды в год равна r, то дюрацией Маколея (Macaulay duration) данного финансового инструмента называется величина

Модифицированная дюрация(modified duration) финансового инструмента определяется равенством

где D – дюрация Маколея,

r – требуемая доходность при начислении процентов дважды в год.