Алексей Лобанов - Энциклопедия финансового риск-менеджмента
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алексей Лобанов - Энциклопедия финансового риск-менеджмента краткое содержание
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).
Энциклопедия финансового риск-менеджмента - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
w – отношение числа дней между расчетной датой и очередным купонным платежом к числу дней в купонном периоде.
Пример 1.18.Найдем доходность к погашению облигации из примера 1.17.
В данном случае
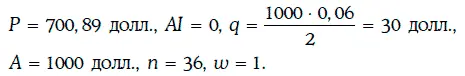
Следовательно, доходность к погашению удовлетворяет уравнению:
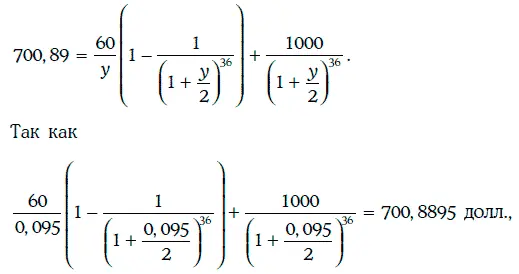
то доходность к погашению облигации равна 9,50 %.
Нетрудно убедиться, что имеют место следующие утверждения:
1) если купонная облигация продается по номиналу, то купонная ставка равна текущей доходности облигации и ее доходности к погашению;
2) если купонная облигация продается с премией, то ее купонная ставка больше текущей доходности, которая, в свою очередь, больше доходности к погашению;
3) если же купонная облигация продается с дисконтом, то ее купонная ставка меньше текущей доходности, которая, в свою очередь, меньше доходности к погашению (см. примеры 1.17 и 1.18).
1.7.3. Доходность к отзыву
Во многих случаях при эмиссии облигаций оговаривается право эмитента выкупить всю эмиссию или некоторую ее часть до установленной даты погашения облигаций. Такие облигации принято называть отзывными (callable bonds). Для отзывных облигаций заранее устанавливается специальный график отзыва, показывающим цены отзыва в зависимости от времени, прошедшего после даты эмиссии; обычно через определенное время после эмиссии цена отзыва устанавливается выше номинала облигации, а затем она постепенно снижается до номинала.
Доходность к отзыву(yield to call) при условии, что расчетная дата приходится на дату купонного платежа, является решением уравнения следующего вида:

где Р – котируемая цена облигации с полугодовыми купонами;
q – полугодовой купонный платеж;
n* – число купонных платежей, остающихся до рассматриваемой даты отзыва;
А* – цена отзыва в соответствующий момент времени.
Пример 1.19.Дана 11 %-ная облигация с полугодовыми купонами номиналом 1000 долл. и сроком погашения 19 лет, продающаяся по цене 1224,07 долл. Определим доходность облигации: а) к погашению; б) к отзыву через 6 лет по цене 1055 долл.; в) к отзыву через 10 лет по номиналу.
Доходность к погашению данной облигации должна удовлетворять следующему уравнению:
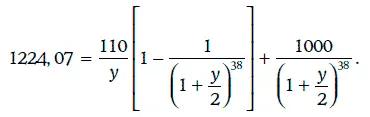
Решив уравнение, получим, что у = 0,0858. Таким образом, доходность к погашению составляет 8,58 %.
Доходность к отзыву через 6 лет является решением уравнения
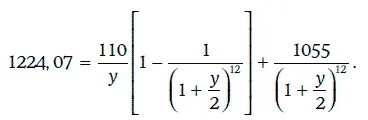
Откуда у = 0,0710, т. е. 7,10 %.
Наконец, доходность к отзыву по номиналу равна 7,74 %, так как должна удовлетворять уравнению
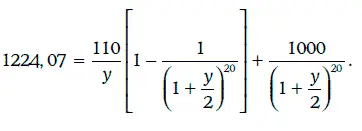
1.7.4. Доходность к продаже
В некоторых случаях по условиям эмиссии держатель облигации имеет право продать облигацию эмитенту по заранее установленной цене, зависящей от времени, прошедшего с момента эмиссии. Такие облигации называют продаваемыми (putable bonds) [15] Другое распространенное название – облигация с офертой.
. Для продаваемых облигаций можно определить доходность к продаже (yield to put) [16] Другое распространенное название – доходность к оферте.
по аналогии с тем, как находится доходность к отзыву для отзывных облигаций.
Если же облигация одновременно является отзывной и продаваемой, то можно рассмотреть доходность до всех предполагаемых дат отзыва и доходность ко всем предполагаемым датам продажи. Наименьшая из всех таких доходностей называется доходностью к «наихудшему» (yield to worst).
1.7.5. Маржа дисконтирования
Мера доходности, называемая маржей дисконтирования (discounted margin), применяется только к облигациям с плавающей купонной ставкой (floating-rate securities). В простейшем случае плавающая купонная ставка определяется в установленные моменты времени по формуле:
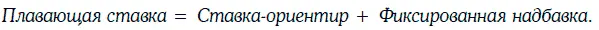
Маржей дисконтирования называют надбавку к ставке-ориентиру, которую держатель облигации ожидает получить за все время существования облигации, если ставка-ориентир не будет отклоняться от своего текущего уровня.
Пример 1.20.Дана 6-летняя облигация с плавающей купонной ставкой номиналом 100 долл. Купонная ставка больше ставки-ориентира на 80 базисных пунктов и определяется каждые 6 месяцев. Определим маржу дисконтирования, если цена облигации 99,31 долл., а текущее значение ставки-ориентира – 10 %.
При определении маржи дисконтирования считается, что ставка-ориентир не меняется с течением времени. Значит, в этом случае полугодовой купонный платеж составит:
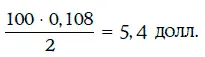
Маржа дисконтирования должна удовлетворять следующему уравнению:
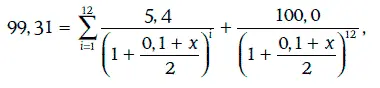
которое можно переписать в виде:
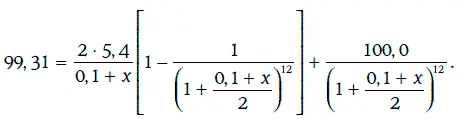
Решив уравнение, получим, что х = 0,0096. Таким образом, маржа дисконтирования составляет 96 базисных пунктов.
1.8. Оценка доходности портфелей облигаций
Для оценки доходности портфелей облигаций чаще всего используются следующие две меры доходности: средневзвешенная доходность и внутренняя доходность.
1.8.1. Средневзвешенная доходность портфеля облигаций
Средневзвешенная доходность портфеля облигаций(weighted average portfolio yield) определяется по формуле:
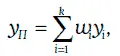
где k – число облигаций в портфеле;
y i – доходность i -й облигации, i = 1, 2, …, k ;
w i – отношение рыночной стоимости i -й облигации к рыночной стоимости всего портфеля, i = 1, 2, …, k.
Пример 1.21.Портфель состоит из двух облигаций с полугодовыми купонами, параметры которых указаны в таблице:
Читать дальшеИнтервал:
Закладка:










