Алексей Лобанов - Энциклопедия финансового риск-менеджмента
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алексей Лобанов - Энциклопедия финансового риск-менеджмента краткое содержание
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).
Энциклопедия финансового риск-менеджмента - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
2. Если случайная величина ξ имеет логнормальное распределение с параметрами а и S, то
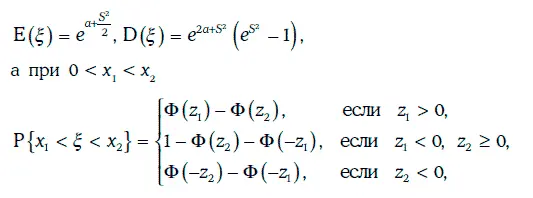
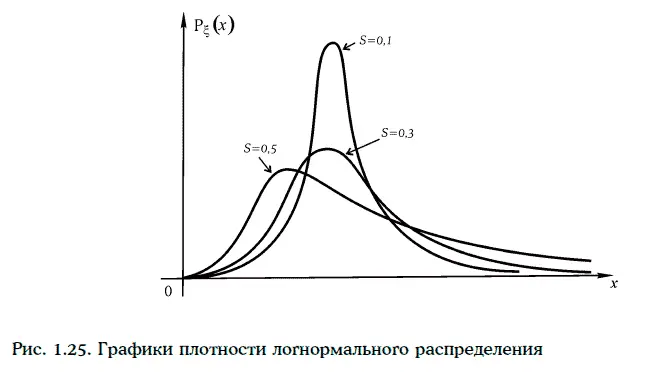

Пример 1.57.Будем считать, что доходность 10-летних облигаций с нулевыми купонами имеет логнормальное распределение с параметрами a = -2,70; S = 0,30.

3. Если две случайные величины распределены логнормально, то их произведение также имеет логнормальное распределение.
1.22.5. Распределение х 2(хи-квадрат)
Говорят, что случайная величина z имеет распределение х 2(chi-squared distribution) с n степенями свободы, если она представима в виде суммы n квадратов взаимно независимых величин со стандартными нормальными распределениями.


Пример 1.58.Даны 10 дневных наблюдений доходности 30-летних казначейских облигаций с нулевым купоном:

Если допустить, что доходность распределена нормально, то оценки математического ожидания и дисперсии доходности можно найти следующим образом:
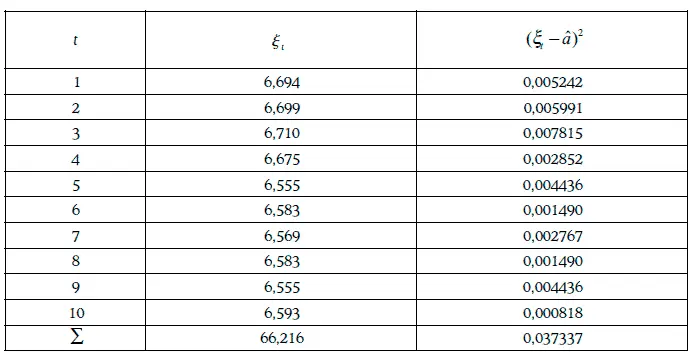
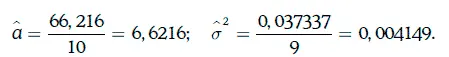
Доверительный интервал для дисперсии доходности с надежностью 96 % можно найти из условия

1.22.6. Распределение Стьюдента
Распределение вероятностей случайной величины

называется распределением Стьюдента (Student’s t-distribution) с n степенями свободы, если случайные величины ξ и η независимы, ξ имеет стандартное нормальное распределение, а η – распределение х 2с n степенями свободы.
1. Если случайная величина t имеет распределение Стьюдента с n степенями свободы, то

Асимметрия распределения Стьюдента равна 0.
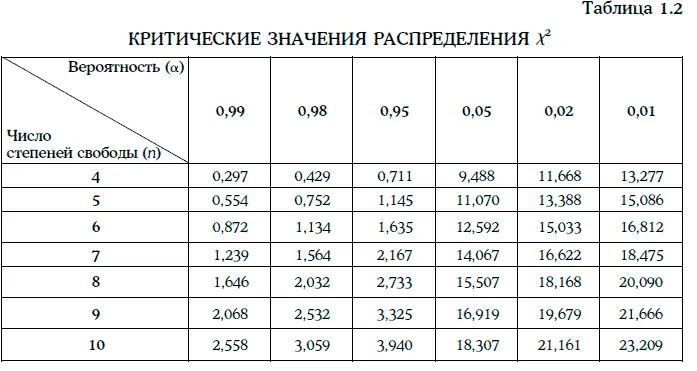
2. При возрастании числа степеней свободы распределение Стьюдента стремится к стандартному нормальному распределению. При этом распределение Стьюдента имеет более тяжелые ветви, чем стандартное нормальное распределение. На рис. 1.26 изображены графики плотности стандартного нормального распределения и распределения Стьюдента с тремя степенями свободы.
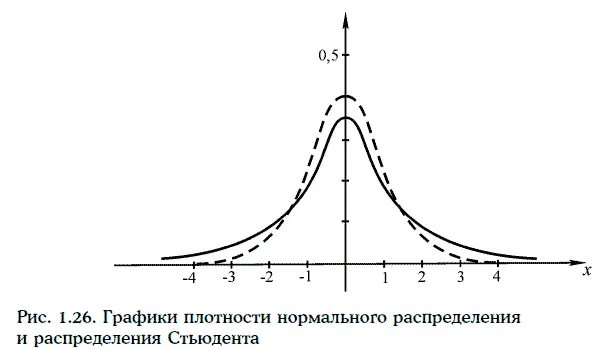
3. Критическим значением распределения Стьюдента с и степенями свободы называют число t a(n), удовлетворяющее условию:
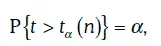
где α – заданная вероятность.
Критические значения распределения Стьюдента указаны в табл. 1.3.
4. Если случайные величины ξ 1, ξ 2…., ξ nвзаимно независимы и распределены нормально с параметрами (а, σ), то случайная величина
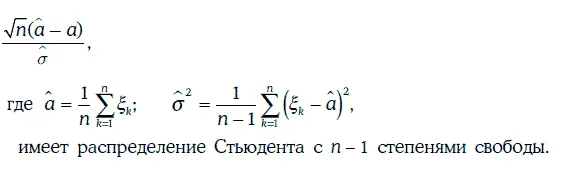
Пример. 1.59.В условиях примера 1.58 найдем доверительный интервал для ожидаемой доходности с надежностью 95 %.
Так как
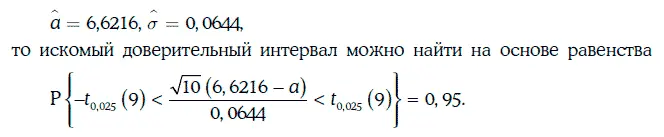

Согласно табл. 1.3, критическое значение распределения Стьюдента t 0,025(9) = 2, 262.
Следовательно,

Таким образом, с надежностью 95 % ожидаемая доходность казначейских облигаций находится между 6,57 и 6,67 %.
1.22.7. Гамма-распределение
Плотность гамма-распределения Г(α, γ) имеет следующий вид:
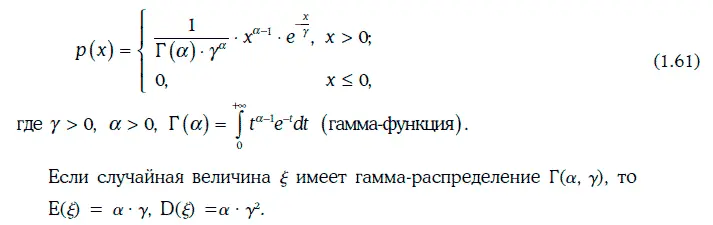
1.22.8. Бета-распределение
Плотность бета-распределения В(α, β) записывается в виде:

Если случайная величина ξ имеет бета-распределение В(α, β), то
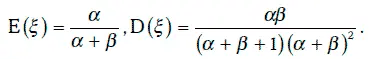
1.22.9. Двумерное нормальное распределение
Плотность двумерного нормального распределения имеет следующий вид:
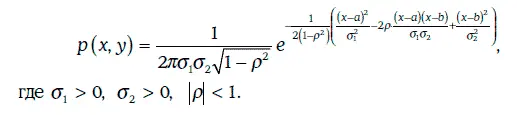

1.23. Расчет волатильности финансовых показателей на основе исторических данных
Волатильность, или изменчивость (volatility), финансовых показателей играет очень важную роль в управлении финансовыми рисками.
Пусть Y t – некоторый финансовый показатель (например, цена или доходность некоторого финансового инструмента), наблюдаемый в день t, t = 0, 1, 2, …, T. Положим
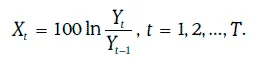
Случайная величина X tпредставляет собой натуральный логарифм относительного изменения этого показателя за один день, выраженный в процентах. Тогда дневную волатильность данного показателя можно оценить следующим образом:
Читать дальшеИнтервал:
Закладка:










