Джин Желязны - Говори на языке диаграмм: пособие по визуальным коммуникациям

Четкие границы. Размеры интервалов должны быть четко обозначены. «Перекрывающиеся» границы (0—10, 10–20, 20–30) не объясняют, к каким интервалам относятся цифры, повторяющиеся по два раза (10, 20). Для непрерывных величин (например, объемов продаж в долларах) предпочтительнее всего следующие границы – менее 10,00 долл., 10,00–19,99 долл., 20,00–29,99 долл. и т. д. Для дискретных величин (количество произведенных автомобилей и т. п.) – менее 10, 10–19, 20–29 и т. д.

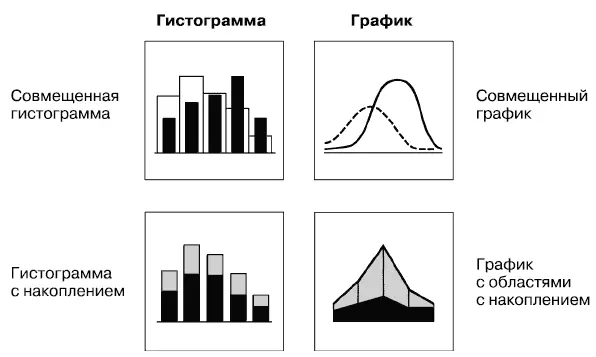
И гистограммы, и графики можно совмещать. Например, для того, чтобы сравнить данные по двум разным годам или сопоставить возрастной состав сотрудников вашей компании и компаний-конкурентов или в отрасли в целом. Кроме того, при иллюстрации конкретных величин можно применять диаграммы с накоплением, чтобы показать вклад каждого параметра в общую сумму[ Внимание! Нельзя применять диаграммы с накоплением, когда частота распределения выражена в процентах. Например, если от 5 до 10 долл. в час зарабатывают 60 % женщин и 50 % мужчин, нельзя сказать, что в целом 110 % населения зарабатывают от 5 до 10 долл. в час.].

Корреляционное сравнение показывает, соответствует ли соотношение двух переменных ожидаемой зависимости. Например, обычно можно ожидать, что более опытный продавец работает эффективнее, чем менее опытный, или что люди с более высоким уровнем образования получают более высокую стартовую заработную плату. Подобные сравнения лучше всего иллюстрируются при помощи точечных (рассеянных) или двусторонних линейчатых диаграмм. Рассмотрим каждый из этих вариантов.

На этой диаграмме мы показываем 16 сделок с точки зрения размера скидок и количества единиц проданного товара. Обычно ожидается, что чем больше скидка, тем выше стимул купить больше товара. Но, как показывает точечная диаграмма, в данном случае подобной корреляции нет.

Точечная диаграмма

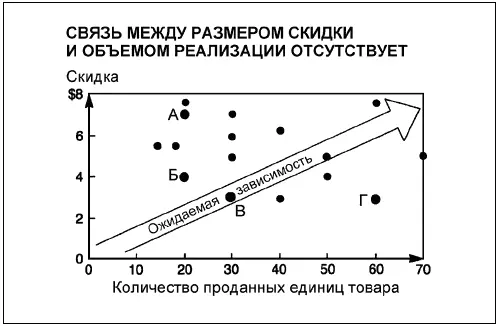
Взгляните, к примеру, на точки А и Б, обозначающие сделки, совершенные двумя продавцами. Оба продали по 20 единиц товара (горизонтальная шкала). Однако А предлагал 7-долларовую скидку, тогда как скидка у Б составляла всего 4 доллара (вертикальная шкала). С другой стороны, продавцы В и Г предлагали одинаковую скидку в 3 доллара, но В продал 30 единиц, а Г — в два раза больше. Как видно, размер предлагаемой скидки слабо влиял или вообще не влиял на объемы продаж.

Если бы между этими параметрами существовала статистически значимая связь (корреляция), точки концентрировались бы вдоль диагональной линии, идущей от левого нижнего угла диаграммы к правому верхнему, что на рисунке показано стрелкой. Подобные стрелки удобно использовать для обозначения предполагаемой модели развития событий. Стрелка может быть направлена вниз, когда вы хотите показать, что объемы продаж возрастают со снижением цен. Не следует путать такую стрелку с математически вычисляемой «линией тренда» – кривой, которая показывает тенденцию изменения величины.

Подобные точечные диаграммы сейчас все шире используются в презентациях, докладах и некоторых деловых журналах. Если вы также собираетесь их применить, позаботьтесь о своих слушателях или читателях и сначала объясните, как читать такой тип диаграммы.

Еще одна проблема, связанная с данным типом диаграмм, – это обозначение точек. Если под каждой точкой подписывать, скажем, имя продавца, это может не только запутать читателя, но и повредить его зрению. Приемлемый вариант – обозначать точки буквами или цифрами, которые соотносятся с полными именами или названиями, приведенными в легенде. Более правильный вариант – использовать двустороннюю линейчатую диаграмму.

Линейчатая диаграмма

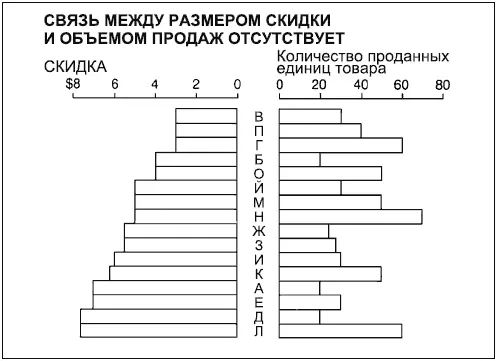
Как видно, при использовании двусторонней линейчатой диаграммы наименование каждого ряда величин, нанесенных на диаграмму, можно вписать между двумя рядами линеек. Кроме того, в таких диаграммах независимые переменные обычно располагают слева – от меньшего значения к большему или наоборот. Если ожидаемая и реальная зависимости совпадают, то линейки справа, обозначающие зависимые переменные, будут зеркальным отражением независимых. Другими словами, низким скидкам будет соответствовать небольшой объем продаж, а высоким – большой. Если же реальная зависимость не соответствует ожидаемой, то два столбца будут отличаться друг от друга, как в приведенном примере.

Подобное использование двусторонней линейчатой диаграммы имеет смысл, только когда мы наносим на чертеж относительно небольшое количество показателей. Если же их от 15 и выше, то гораздо лучше составить более компактную рассеянную диаграмму, не подписывая на ней каждую точку.

Если у двусторонней линейчатой диаграммы нет никаких разновидностей, то у точечной диаграммы их несколько.

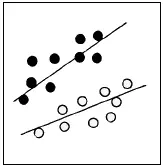
Совмещенная точечная диаграмма показывает корреляцию между двумя разными показателями или состояниями одного и того же показателя в разное время. Хотя в основном в такой диаграмме используются закрашенные и незакрашенные точки, можно применить и другие символы: квадраты, треугольники или звездочки.

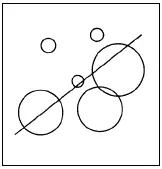
В пузырьковой диаграмме присутствует третья переменная, обозначаемая разной величиной точек. К примеру, две шкалы могут отражать продажи и прибыли, а размер точек – относительный объем активов каждой компании в отрасли.

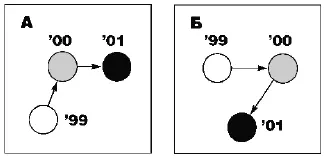
Временная точечная диаграмма показывает изменения корреляции с течением времени. Не пытайтесь изобразить все эти изменения в рамках одной сетки, лучше составьте несколько диаграмм.

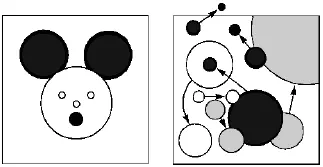
Внимание! Старайтесь делать точечные диаграммы проще – иначе может получиться Микки-Маус или схема звездных войн.

Итак, у нас есть пять основных типов сравнения – они выражаются в формулировках главной идеи, основанной на исходных данных, – и соответствующие им типы диаграмм.