Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Как мы уже убедились, графический способ решения уравнения регрессии в программе Excel позволяет довольно существенно экономить время. Однако у этого способа есть и один весьма существенный недостаток, обусловленный тем, что при этом не проводится оценка статистической значимости как в целом уравнения регрессии, так и его коэффициентов.

Таким образом, графический способ решения уравнения регрессии целесообразно использовать на этапе предварительного отбора уравнений регрессии, имеющих наиболее высокий коэффициент детерминации. После отбора уравнения регрессии с высоким коэффициентом детерминации в Excel его нужно решить, используя в Пакете анализа опцию РЕГРЕССИЯ (см. алгоритм действий № 3). Однако решение уравнения регрессии, аппроксимирующего фактические данные степенным трендом, имеет определенную специфику. В отличие от линейного тренда уравнение регрессии решается не относительно имеющихся исходных данных, а по отношению к их логарифмам. Объясняется это тем, что уравнение регрессии со степенным трендом относится по оцениваемым параметрам к нелинейным моделям, но путем логарифмирования его можно привести к линейному виду.

В результате уравнение регрессии для степенного тренда (см. табл. 2.7) приобретет следующий вид:

Следует иметь в виду, что приведение нелинейной функции к линейному виду с помощью логарифмирования используется очень часто, хотя это и приводит к некоторым коллизиям. Вот что пишут по этому поводу Е.М. Четыркин и И.Л. Калихман: «Однако такое преобразование приводит к тому, что оценка параметров базируется не на минимизации суммы квадратов отклонений, а на минимизации суммы квадратов отклонений в логарифмах…Следствием этого является некоторое смещение оценок параметров, получаемых обычным (линейным) МНК» [8] Четыркин Е.М., Калихман И.Л. Вероятность и статистика. М.: Финансы и статистика, 1982. С. 255. .

Далее параметры этого уравнения регрессии находятся согласно формулам (2.1.4) и (2.1.5) либо решаются с помощью соответствующей компьютерной программы.

Поэтому прежде чем приступить к выполнению алгоритма действий № 3 «Как решить уравнение регрессии в Excel», нужно взять натуральные логарифмы (логарифмы, основанием которых служит число е = 2,71828) как от независимой переменной х — порядковый номер месяца, так и от зависимой переменной у — курс доллара. В Excel для этих целей можно воспользоваться функцией LN. Далее поступаем в полном соответствии с алгоритмом действий № 3, а данные, полученные после решения уравнения регрессии, занесем в табл. 2.8.

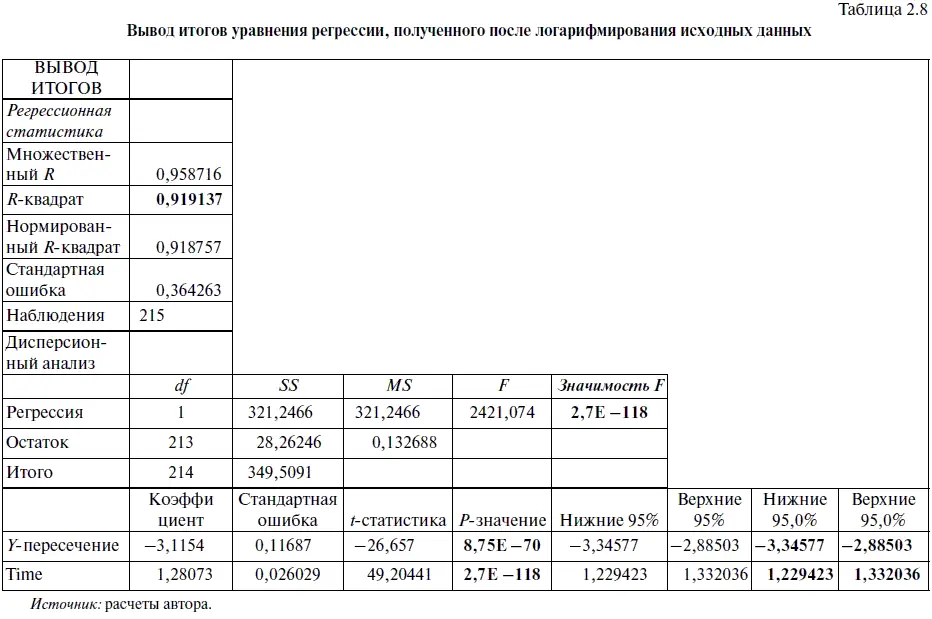
Согласно алгоритму действий № 4 «Оценка статистической значимости уравнения регрессии и его коэффициентов», проведем проверку статистической значимости этого уравнения регрессии. При этом выделим в табл. 2.8 все важнейшие пункты жирным шрифтом. В результате мы приходим к выводу, что у нас получились статистически значимыми уравнение регрессии и его коэффициенты как при 95 %-ном, так и 99 %-ном уровне надежности. Правда, поскольку уравнение регрессии мы решили относительно натуральных логарифмов, взятых от исходных данных, то в результате оно приобрело следующий вид:

Ln Y = -3,1154 + 1,28073 lп Х

Согласно последнему уравнению регрессии, прогноз курса доллара рассчитывается на основе логарифмов, взятых от исходных данных. Например, прогноз относительно апреля 2010 г. вычисляется следующим образом:

Ln Y = -3,1154 + 1,28073 × 5,370638 = 3,762939,

где 5,370638 = ln (215) — натуральный логарифм от порядкового номера апреля 2010 г. — 215.

Отсюда находим (в Excel потенцирование натуральных логарифмов производится с помощью функции ЕХР), что прогноз курса доллара на апрель 2010 г. равен

Y = ЕХР (3,762939) = 43,07482.

После проведения соответствующих преобразований уравнение регрессии приобретет следующий вид:

Y = ЕХР (-3,1154 + 1,28073 ln Х) = 0,044361 × X ^1,28073.

С помощью последнего уравнения регрессии можно делать расчет прогнозов непосредственно от исходных данных, а не от их натуральных логарифмов. В результате можно получить следующий прогноз курса доллара на апрель 2010 г.:

Y =0,044361 × 215^1,28073,

где 215 — порядковый номер апреля 2010 г. (июнь 1992 г. — 1).

Несмотря на то что коэффициент детерминации у степенного уравнения регрессии выше, чем у линейного, однако, например, относительно апреля 2010 г. прогноз по этому уравнению регрессии весьма сильно отклоняется от фактического курса доллара, как впрочем, и во многих других случаях. Судя по табл. 2.9, с января 2009 г. по апрель 2010 г. отклонения от прогноза (остатки), сделанного по уравнению регрессии Y расч= 0,044361 — X ^1,28073, колебались в диапазоне от -3,7954 руб. до -13,7862 руб., что свидетельствует о невысокой точности этой прогностической модели.

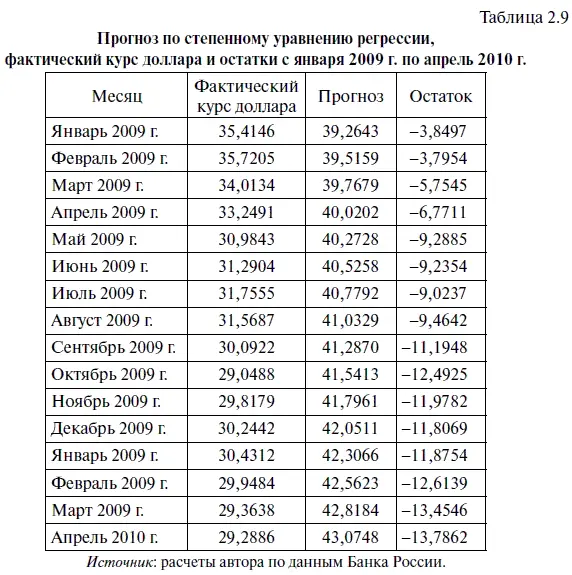
При этом средняя абсолютная ошибка прогноза по модулю для степенной статистической модели (см. формулу (2.20)) оказалась равна 5 руб. 92,4 коп. Следовательно, этот показатель для анализируемой модели оказался на 30 коп. больше, чем у линейной модели. В свою очередь средняя относительная ошибка по модулю в процентах (см. формулу (2.20)) для степенной модели оказалась равна 31,10 %, т. е. на 7,78 процентных пункта ниже, чем у линейной модели. Более того, если построить график остатков по степенной прогностической модели (рис. 2.6), то легко обнаружить, что на нем наблюдается несколько локальных трендов. А это — как мы говорили ранее — наглядно свидетельствует о нестационарности остатков.

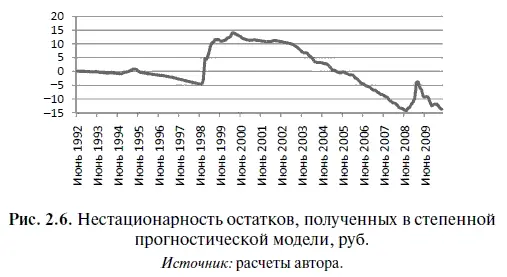
Отсюда можно сделать вывод, что не только линейная модель, но и степенная модель, в которой в качестве независимой переменной использовался фактор времени (порядковый номер месяца), оказались непригодны для прогнозирования курса доллара. Все это заставляет нас продолжить поиск адекватной прогностической модели.

1. В чем суть метода наименьших квадратов, как этот метод можно представить графически?

2. Перечислите все пункты алгоритма действий, которые необходимо выполнить при решении уравнения регрессии в Microsoft Excel.

3. Какое уравнение регрессии (при прочих равных условиях) точнее: то, которое имеет коэффициент детерминации ( R -квадрат) = 0,757, либо то, у которого R -квадрат равен 0,978? Объясните почему?