Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Y t= с+b 1 Y t- 1 +b 2 Y t- 2 +b 3 Y t- 3 +e t, (3.2)

где Y t- 1, Y t- 2и Y t- 3— независимые (факторные) переменные с лагом в один, два и три месяца;

b 1 , b 2и b 3— соответствующие коэффициенты регрессии при лаговых переменных.

Помимо авторегрессионных моделей нам необходимо также познакомиться и с моделями со скользящим средним в остатках, которые в англоязычной литературе обычно называются словосочетанием Moving Average. Полезность моделей со скользящим средним в остатках обусловлена тем, что для стационарного ряда предсказываемую переменную Y t можно представить в виде линейной функции прошлых ошибок (отклонений прогнозов от их фактических значений). Следует иметь в виду, что термин «скользящая средняя» в данном случае не является синонимом скользящей средней, применяемой, например, для сезонного сглаживания уровней динамического ряда. При этом модель со скользящим средним в остатках 1-го порядка кратко обозначается как МА(1), а в виде формулы она приобретает следующий вид:

Объединение в одной модели авторегрессионного процесса AR и модели со скользящим средним в остатках МА приводит к созданию более экономичной модели с точки зрения количества используемых параметров. Эту объединенную модель в англоязычной литературе кратко называют ARMA. Эта аббревиатура произошла от словосочетания Auto Regressive — Moving Average, что в переводе означает «авторегрессионный процесс со скользящим средним в остатках».

Порядок в этой модели в буквенной форме принято обозначать как ARMA( p, q), где р — величина порядка авторегрессионного процесса, a q — величина порядка процесса со скользящим средним в остатках. Например, модель ARMA(2; 1) фактически представляет собой комбинацию модели AR(2) с моделью МА(1), т. е. в одной модели объединена авторегрессионная модель 2-го порядка с моделью со скользящим средним в остатках 1-го порядка. В результате модель ARMA(2; 1) приобретает следующий вид:

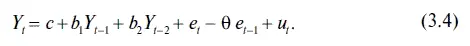
Чтобы объединенная модель ARMA(2; 1) была более понятна, ее можно задать в виде двух уравнений. Так, для AR(2) формула будет иметь вид

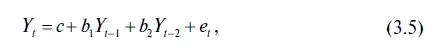
в то время как уравнение для МА(1) можно представить в следующем виде:

Следовательно, формулу (3.4) модели ARMA(2; 1) можно получить путем вычитания из формулы (3.5) расчетного параметра Ое, из левой части уравнения (3.6).

При практическом построении модели ARMA(/? q) наиболее трудным является определение параметров ряд, т. е. определение оптимального количества лагов. При этом инструментами для нахождения соответствующих лаговых переменных являются автокорреляционная функция и частная автокорреляционная функция.

Программа EViews позволяет довольно быстро найти оптимальные параметры р и q для модели ARMA, для этого используется коррелограмма зависимости между различными лагами временного ряда с ежемесячными курсами американского доллара к российскому рублю.

С этой целью загрузим в EViews ежемесячные данные по курсу доллара (столбец с данными обозначим как USDollar) в соответствии с алгоритмом действий № 2 «Импорт данных и создание рабочего файла в EViews», изложенным в главе 1.

Далее строим коррелограмму, тем более что в EViews сделать это довольно просто. С этой целью в Workfile (рабочем файле) этой программы открываем файл USDollar. После чего в файле USDollar нам необходимо выбрать опции VIEW/CORRELOGRAM, а в появившемся окне (рис. 3.1) CORRELOGRAM SPECIFICATION (спецификация коррелограммы) оставить заданные по умолчанию опцию LEVEL (исходный уровень) и опцию LAGS ТО INCLUDE (максимальная величина лага, включенного в коррелограмму). В результате у нас получится коррелограмма исходных уровней (фактических значений курса доллара) временного ряда USDollar с величиной лага от 1 до 36.

Если бы мы выбрали, например, опцию 1ST DIFFERENCE (разница исходных уровней 1-го порядка) или 2ND DIFFERENCE (разница исходных уровней 2-го порядка), тогда была бы построена коррелограмма не исходных уровней временного ряда, а соответственно их первых и вторых разностей. Например, исходный уровень для курса доллара по состоянию на апрель 2010 г. был равен 29,2886 руб. В то время как разница исходных уровней 1-го порядка на эту же дату оказалась равна -0,0752 руб. (т. е. по сравнению с прошлым месяцем курс доллара снизился на 7,52 коп.), а разница исходных уровней 2-го порядка составила 0,5094 руб. (т. е. падение курса доллара по сравнению с предыдущим месяцем уменьшилось на 50,94 коп.).

В полученной коррелограмме (см. табл. 3.1) можно увидеть, как меняются коэффициенты автокорреляции ( Autocorrelation, или АС) и частной автокорреляции (Partial Correlation, или РАС) в зависимости от изменения величины лага. Корреляционную зависимость между последовательными уровнями временн о го ряда называют автокорреляцией уровней ряда. Так, коэффициент автокорреляции уровней первого порядка измеряет корреляционную зависимость между динамикой курса доллара временного ряда t и динамикой курса доллара временного ряда t- 1, т. е. в нашем случае измеряется коэффициент автокорреляции при лаге в один месяц. В свою очередь коэффициент автокорреляции уровней второго порядка измеряет зависимость между динамикой курса доллара временного ряда t и динамикой курса доллара временного ряда t- 2, т. е. при лаге в два месяца. И так далее, вплоть до коэффициента автокорреляции уровней 36-го порядка, измеряющего зависимость между динамикой курса доллара временн о го ряда t и динамикой курса доллара временного ряда t- 36, т. е. с лагом в 36 месяцев.

При этом коэффициент автокорреляции уровней k -го (т. е. 1-го, 2-го…., 36-го) порядка находится в EViews по следующей формуле: