Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Чтобы проверить наше последнее предположение, нам пришлось создать две дополнительные фиктивные переменные: DUMMY09 и DUMMY10. При этом DUMMY09 принимает нулевые значения с августа 1992 г. и до августа 1998 г. (включительно), а область нулевых значений — для DUMMY10 с августа 1992 г. до сентября 1998 г. (включительно). Во всех последующих наблюдениях вплоть до апреля 2010 г. эти фиктивные переменные равны единице. Две дополнительные фиктивные переменные потребовались нам для создания новых переменных наклона USDOLLAR(-1) × DUMMY10 и USDOLLAR(-2) × DUMMY09. После чего в диалоговое мини-окно EQUATION ESTIMATION была введена формула в следующем виде: USDOLLAR USDOLLAR(-1) USDOLLAR(-2) DUMMY DUMMY10 × USDOLLAR(-1) DUMMY09 × USDOLLAR(-2).

В результате мы получили вывод данных для уравнения регрессии с новыми фиктивными переменными наклона. Судя по табл. 5.15, все коэффициенты в этом уравнении регрессии оказались статистически значимыми, поскольку уровень их значимости оказался равен нулю. Следовательно, нулевую гипотезу об отсутствии в динамике курса доллара в августе 1998 г. структурных изменений сдвига и отсутствии в сентябре и октябре 1998 г. структурных изменений наклона можно считать опровергнутой с 1 %-ным уровнем значимости. Это и позволяет нам взять за основу альтернативную гипотезу, что эти структурные изменения имели существенное значение.

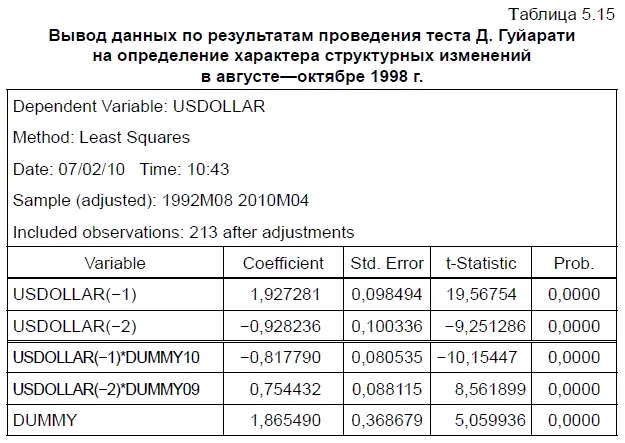
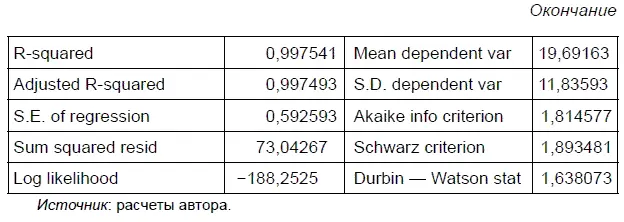
Из таблицы 5.15 можно сделать вывод, что до августа 1998 г. динамика курса доллара описывалась трендом, имеющим следующую формулу:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) (5.9.1)

При этом интерпретация уравнения (5.9.1) была следующая: во-первых, рост на 1 руб. курса доллара в текущем месяце способствовал повышению курса доллара в будущем месяце в среднем на 1,927 руб.; во-вторых, рост на 1 руб. курса доллара в прошлом месяце способствовал снижению курса доллара в будущем месяце в среднем на -0,928 руб.

В августе 1998 г., когда произошел структурный сдвиг, формула тренда приобрела иной вид:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) + 1,865 × DUMMY (5.9.2)

Интерпретация формулы (5.9.2) аналогична предыдущей, за исключением того, что появление в уравнении фиктивной переменной DUMMY свидетельствует о единовременном повышении курса доллара в августе 1998 г. на 1,865 руб.

В сентябре 1998 г., когда имело место первое структурное изменение наклона, формула тренда снова изменилась:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) + 0,754 × USDOLLAR(-2) × DUMMY09 + 1,865 × DUMMY

(5.9.3)

Формула (5.9.3) отличается от уравнения (5.9.2) тем, что у нее появилась фиктивная переменная наклона USDOLLAR(-2) × DUMMY09, показывающая увеличение коэффициента регрессии у переменной

USDOLLAR(-2) на 0,754. Следовательно, с этого месяца вклад переменной USDOLLAR(-2) в динамику курса доллара с учетом структурного наклона, стал следующим: рост на 1 руб. курса доллара в прошлом месяце способствовал снижению курса доллара в будущем месяце в среднем на -0,174 руб.

В октябре 1998 г. после второго структурного изменения наклона наша формула приобрела следующий вид:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,818 × USDOLLAR(-1) × DUMMY10- 0,928 USDOLLAR(-2) + 0,754 × USDOLLAR(-2) × DUMMY09 + 1,865 × DUMMY

(5.9.4)

Формула (5.9.4) отличается от предыдущей лишь тем, что у нее появилась фиктивная переменная наклона USDOLLAR(-1) × DUMMY10, которая показывает уменьшение коэффициента регрессии у переменной USDOLLAR(-1) на -0,818. Следовательно, с октября 1998 г. вклад переменной USDOLLAR(-2) в динамику курса доллара изменился таким образом: рост на 1 руб. курса доллара в текущем месяце способствовал повышению курса доллара в будущем месяце в среднем на 1,109 руб.

Следует иметь в виду, что формула (5.9.4) отличается, например, от формулы (3.4), описывающей аналогичный период, поскольку у этих формул разное число оцениваемых параметров.

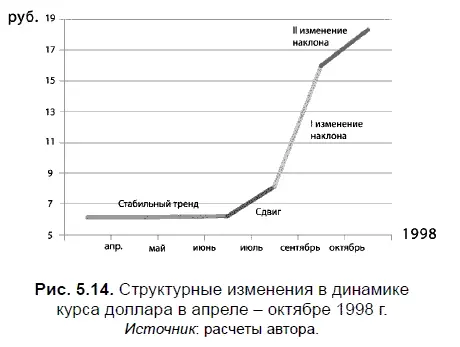
На диаграмме, представленной на рис. 5.14, изображен график, наглядно показывающий характер структурных изменений в динамике курса доллара, произошедших во время кризиса 1998 г. В частности, здесь можно увидеть как структурный сдвиг, произошедший в августе 1998 г., так и первое, и второе структурные изменения наклона, имевшие место в сентябре и октябре 1998 г.

Американский экономист Д. Гуйарати для оценки структурных изменений в динамике тренда, происходящих в момент времени t*, предложил оценивать параметры следующего уравнения регрессии с фиктивными переменными:

Y t = а + b × Z t+ с × t + d × (Z t× t) + е, (5.10)

где Y t— зависимая переменная; t — время;

а, b, с, d — параметры уравнения регрессии;

е — ошибка (остатки);

Z t— фиктивная переменная, которая при t < t' равна нулю, а при t ≥ t' равна единице.

Следовательно для момента времени t < t' мы получим следующее уравнение регрессии:

Z t= 0 => Y,= а + b × 0 + с × t + d × (0 × t) + e=>Y t= a+ c × t + e. (5.10.1)

Соответственно для момента времени t> f уравнение примет такой вид:

Z t= 1 => Y t= a+b × l+c × t + d × (1 × t ) + е =>

=> Y t= (a+b) + (c+d) × t + e. (5.10.2)

Сравнив уравнение (5.10.1) с уравнением (5.10.2), нетрудно прийти к выводу, что при Z t= 1 свободный член уравнения а 2 =(а+ b), а коэффициент регрессии — c 2 × t = (c+d) × t. Соответственно при Z t= 0 свободный член уравнения а 1 = а, а коэффициент регрессии — с 1 × t= с × t. Таким образом, параметр b можно рассматривать как разницу между а 1и а 2, т. е. между свободными членами уравнений (5.10.1) и (5.10.2). В свою очередь параметр d следует рассматривать как разницу между c 1и с 2, т. е. между коэффициентами регрессии уравнений (5.10.1) и (5.10.2). Следовательно, параметр b оценивает структурный сдвиг, а параметр d — структурное изменение наклона в уравнении регрессии, произошедшее в момент времени t' . Оценку параметров bud можно провести, решив уравнение регрессии, а затем оценив их значимость при помощи t- критерия Стьюдента.

Подробности по этой теме можно узнать, ознакомившись с соответствующей литературой [17] См., например: Эконометрика. С. 327–334. .

Таким образом, с помощью метода, предложенного американским экономистом Д. Гуйарати, нам удалось выяснить, что во временн о м ряде по ежемесячному курсу доллара, охватывающем период с июня 1992 г. по апрель 2010 г., после августовского дефолта 1998 г. произошли следующие структурные изменения: во-первых, в августе 1998 г. произошел структурный сдвиг; во-вторых, в сентябре 1998 г. имело место первое структурное изменение наклона (изменился коэффициент регрессии факторной переменной с лагом в два месяца); в-третьих, в октябре 1998 г. имело место второе структурное изменение наклона (изменился коэффициент факторной переменной с лагом один месяц).