Александр Волошинов - Математика и искусство

Принцип двойственности: теорема Паскаля (а) и теорема Брианшона (б)

И в заключение вновь перейдем от математики к искусству. Рождению проективной геометрии во многом способствовали геометрические исследования художников Возрождения. А появившись на свет, проективная геометрия стала теоретическим фундаментом искусства перспективы. Важную роль при построении перспективных изображений играет теорема Дезарга. Мы остановимся на двух приложениях этой теоремы к теории перспективы.

Теорема Дезарга и способ архитекторов. Способ-архитекторов, который мы применили в предыдущей главе для построения перспективы интерьера комнаты и перспективы параллелепипеда (см. с. 282), состоит, по существу, в построении двух точек: точки схода изображаемой линии и точки пересечения этой линии с основанием картины. Зная эти две точки, мы можем построить перспективное изображение данной линии. Метод построения точки схода на перспективе был нами разобран на с. 279, доказательство его справедливости очевидно из рисунка на с. 281. А вот найти точку пересечения образа данной линии с основанием картины позволяет нам теорема Дезарга.

Обратимся для определенности к рисунку на с. 282. Прежде всего заметим, что любую фигуру, состоящую из прямых линий, можно разбить на соответствующее число треугольников. Рассмотрим треугольник ABC на плоскости Т (рис. б) и его перспективное изображение треугольник abc на плоскости К (рис. а). По теореме Дезарга соответственные стороны этих треугольников пересекаются в одной точке на основании картины tt. Именно поэтому в наших построениях мы продолжили сторону ВС до пересечения с линией основания tt в точке М (рис. б), а затем перенесли эту точку ни линию tt в плоскости К. Так мы нашли неизвестную нам точку пересечения образа линии ВС с линией основания tt (точка m на рис. а). Аналогично найдена и точка п. Зная точки пересечения m, a, n и их точки схода F lи F 2, легко построить перспективу прямоугольника ABCD.

Теорема Дезарга и недоступные точки схода. Случается, что при построении перспективного изображения художник, а еще чаще архитектор сталкиваются с такой трудностью: точка схода некоторой линии оказывается за пределами картины (чертежа). Покажем, как теорема Дезарга может помочь в этом случае.

Пусть на плоскости картины К даны две прямые а и b, идущие в недоступную точку схода (в качестве одной из таких прямых чаще всего выступает линия горизонта). Требуется через некоторую точку С∈К провести прямую с в недоступную точку схода. Выберем на плоскости К произвольную точку L и проведем через эту точку три произвольных луча l 1, l 2, l 3. Лучи l 1, и l 3пересекут прямые а и b в точках А, В и А', В' соответственно. Через точку С проведем прямые МА и СВ, пересекающие луч l 2в точках М и N. Наконец, проведем прямые МА' и NB' до пересечения в точке С'. Как следует из теоремы Дезарга, прямая с, проходящая через точки С и С', пересекается с прямыми а и b в одной точке, т. е. прямая с и является искомой прямой, идущей в недоступную точку схода.

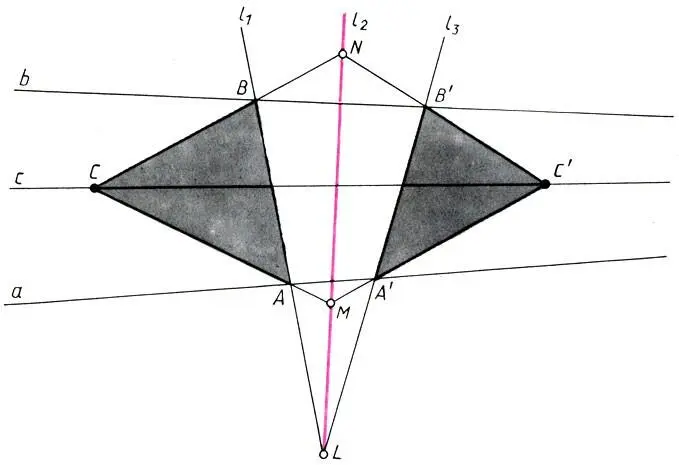
Проведение прямой с в недоступную точку схода с помощью теоремы Дезарга

Мы познакомились с геометрическими методами отображения трехмерного пространства на плоскость картины. Методы эти составляют предмет изучения самостоятельной науки — начертательной геометрии, которая в свою очередь стимулировала развитие еще одной ветви математики — проективной геометрии. Но эти же геометрические методы живут полнокровной жизнью и в искусстве живописи. Они помогают художнику разрешать извечный парадокс искусства живописи: заставить зрителя в плоском холсте, покрытом красками, увидеть реальный трехмерный мир, окружающий человека. В разные эпохи эта "вечная" проблема живописи решалась по-разному, в том числе и разными геометрическими методами, в чем легко убедиться, прочитав следующую главу.

Геометрия и живопись... Пути науки и искусства переплетались в них на протяжении столетий. Геометрия дарила живописи новые изобразительные возможности, обогащала язык живописи, а живопись эпохи Возрождения стимулировала исследования по геометрии, дала начало проективной геометрии. Сейчас нам предстоит взглянуть на геометрию с неожиданной, быть может, стороны. Мы увидим, что геометрия, будучи могучей ветвью древа математики, является в то же время и тем связующим стержнем, который проходит через всю историю живописи.

В самом деле, существуют три принципиальных геометрических метода отображения трехмерного пространства на двумерную плоскость картины: метод ортогональных проекций, аксонометрия и перспектива (см. рис. на с. 277). Перспектива, как явствует из рисунка, может быть прямой или обратной. Все эти принципиальные возможности изображения пространства на плоскости были реализованы в искусстве живописи, причем в разных пластах художественной культуры каждый из этих методов находил свое наиболее полное и чистое выражение. Так, система ортогональных проекций составила геометрическую основу живописи

Древнего Египта; аксонометрия (параллельная перспектива) характерна для живописи средневекового Китая и Японии; обратная перспектива — для фресок и икон Византии и Древней Руси; прямая перспектива — это геометрический язык ренессансной живописи, а также станковой и монументальной живописи европейского искусства XVII века и русского искусства XVIII- XIX веков.

Итак, ортогональные проекции — аксонометрия — перспектива. Именно по такой схеме шло развитие геометрии живописи. Видимо, простота метода прежде всего определяла его положение в этой схеме. Метод ортогональных проекций как наиболее простой занял в ней первое место. Ортогональные проекции передавали без искажений контуры реальных предметов, а идея метода, как справедливо заметил Леонардо да Винчи (см. с. 274), была подсказана человеку самой природой: тень, отброшенная вечерним солнцем на стену, и была первой картиной, нарисованной этим методом. Однако ортогональные проекции никак не передавали глубину реального пространства, поэтому уже в искусстве Древнего Египта появились робкие ростки аксонометрии.

Аксонометрия при надлежащем выборе точки зрения передавала без искажений фронтальную плоскость изображаемого предмета; она давала представление о глубине пространства, хотя и трудно было понять, сколь протяженна эта глубина. Строгий математический взгляд на аксонометрию как центральную проекцию с бесконечно удаленным центром сложился сравнительно недавно, в XVIII веке, в трудах немецкого математика и философа Иоганна Генриха Ламберта (1728- 1777). Однако как нестрогий метод изображения пространства на плоскости аксонометрия, именуемая тогда вольной перспективой, известна давно. Начиная с Птолемея (II в.) и вплоть до XVIII века (до появления начертательной геометрии) планы городов изображались в вольной перспективе, как бы с высоты птичьего полета. (Этот принцип и сегодня широко используется на туристских схемах.)