Александр Волошинов - Математика и искусство

Разумеется, проективная геометрия развилась не вдруг с появлением трактата Понселе. Известны три важнейшие предтечи проективной геометрии — три теоремы элементарной геометрии, которые не содержат в условиях метрических характеристик. Первая теорема известна с глубокой древности и носит имя александрийского геометра III века Паппа.

Теорема Паппа. Пусть l и m — две прямые на плоскости; А, В, С — различные точки прямой l, а А', В', С' — различные точки прямой m. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, С А' и С'А принадлежат одной прямой. Проективный характер теоремы Паппа очевиден: в ней фигурируют только точки, прямые и их пересечения; поэтому теорема Паппа остается справедлива при любом проективном преобразовании.

Через 1200 лет после Паппа шестнадцатилетний юноша Блез Паскаль (1623-1662) опубликовал свое лучшее математическое сочинение "Трактат о конических сечениях". В трактате Паскаль доказал теорему, которую он назвал Hexagramma mysticum (Волшебный шестиугольник) и которую он украсил почти 400 следствиями. Теорему Паскаля можно считать своего рода обобщением теоремы Паппа на случай конических сечений *, которые, как и прямые, обладают проективными свойствами.

*( Коническими сечениями (линиями второго порядка) называют эллипс (и его частный вид — окружность), параболу и гиперболу — линии, которые могут быть получены как сечения прямого кругового конуса. В последнем легко убедиться, посветив обычным карманным фонариком (световой конус) на стену. Когда фонарик перпендикулярен стене, мы видим окружность, затем при наклоне фонарика — эллипс. Когда одна из образующих светового конуса станет параллельна стене, мы Увидим параболу и, наконец, при больших углах наклона — гиперболу. Математическое доказательство этих результатов принадлежит выдающемуся античному математику Апполонию из Перги. )

Теорема Паскаля. Пусть А, В, С, А', В', С' — шесть точек, принадлежащих некоторому коническому сечению. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, СА' и С'А принадлежат одной прямой. Существует и другая формулировка теоремы Паскаля, в которой ее связь с теоремой Паппа не столь очевидна: три точки пересечения противоположных сторон шестиугольника, вписанного в коническое сечение, лежат на одной прямой (см. с. 294). Еще раз подчеркнем, что теорема Паскаля справедлива для любого конического сечения (окружности, эллипса, параболы и гиперболы). Более того, при надлежащем определении касательной в точке конического сечения теорема Паскаля будет выполняться в том случае, когда не все из шести точек различны.

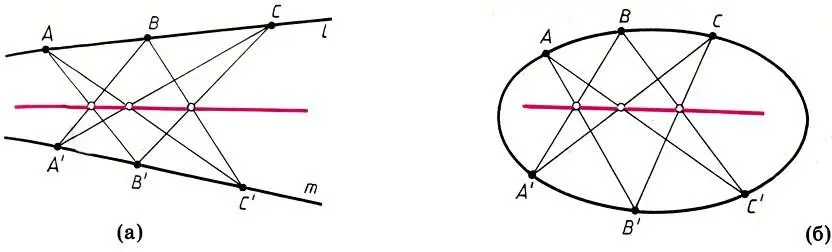
Теорема Паппа (а) и теорема Паскаля (б)

Наконец, третья теорема — одна из важнейших теорем проективной геометрии — носит имя Дезарга, который вместе с Понселе разделяет славу создания проективной геометрии.

Теорема Дезарга. Пусть ABC и А'В'С — два треугольника (необязательно лежащие в одной плоскости), такие, что прямые АА', ВВ' и СС', соединяющие соответственные вершины треугольников, сходятся в одной точке S. Тогда точки пересечения соответственных сторон этих треугольников АВ и А'В', ВС и В'С', СА и С'А' лежат на одной прямой. Плоский вариант теоремы Дезарга, как и теоремы Паппа и Паскаля, отнюдь не очевиден, тогда как ее пространственный вариант настолько прозрачен, что просто удивительно, как художники Возрождения, так много занимавшиеся теорией перспективы, не "заметили" его.

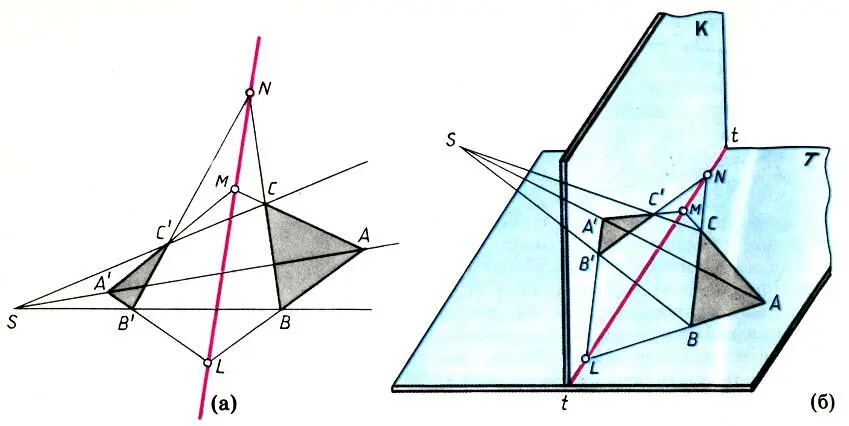
Плоский (а) и пространственный (б) варианты теоремы Дезарга

В самом деле, пусть треугольник ABC лежит в горизонтальной плоскости Т, треугольник А'В'С' есть его изображение на картинной плоскости К и точка S — центр проектирования. Прямые, соединяющие соответственные вершины этих треугольников,- это "лучи зрения", а ΔА'В'С есть сечение "пирамиды зрения" с основанием ABC и вершиной в точке S. Соответственные стороны АВ и А'В' расположены на грани SAB "пирамиды зрения", т. е. лежат в одной плоскости и пересекаются в некоторой точке L. Но точка L одновременно принадлежит прямым АВ и А'В'. Значит, она одновременно принадлежит плоскости Т и плоскости К, т. е. лежит на линии пересечения этих плоскостей — прямой tt. Аналогично доказываем, что и точка пересечения сторон АС и А'С (точка М) и сторон ВС и В'С (точка N) лежат на той же прямой tt. Следовательно, все три точки L, М, N лежат на одной прямой. Пространственная теорема Дезарга доказана.

Для доказательства плоской теоремы Дезарга достаточно ΔА'В'С', лежащий в картинной плоскости К, спроектировать на плоскость Т из двух центров проекции S и S 1определяющих прямую S 1S'. В результате на плоскости Т мы получим два треугольника: ABC и А'В'С. Поскольку прямые S 1A" и SA лежат в одной плоскости, то точки А" и А будут лежать на одной прямой S'A — линии пересечения этой плоскости с плоскостью Т (аналогично для точек В" и B, а также С" и С). Следовательно, прямые, соединяющие соответственные вершины треугольников ABC и А"В"С", пересекаются в одной точке S' т. е. удовлетворяют условию теоремы Дезарга. Для каждой из пар треугольников: ΔА'В'С' и ΔАВС, а также ΔА'В'С' и ΔА"В"С" -справедлива пространственная теорема Дезарга. Более того, так как в каждой паре этих треугольников имеется один й тот же ΔА'В'С', то всякий раз все три соответственные стороны этих треугольников будут пересекаться в одной точке. Так мы получим точки L, М и N, лежащее на прямой tt, т. е. придем к плоской теореме Дезарга.

Оба доказательства теоремы Дезарга настолько просты и изящны, что трудно было удержаться от соблазна привести их здесь. Но дело не только в этом. Мы доказали плоскую теорему Дезарга с помощью ее пространственного аналога, т. е. при помощи пространственных построений. Как показал в конце XIX века Д. Гильберт, без выхода из плоскости в пространство вообще невозможно доказать плоскую теорему Дезарга методами проективной геометрии (без привлечения метрических понятий). Следовательно, если задаться целью разрабатывать плоскую проективную геометрию лишь средствами плоскости, не используя пространство, то мы обязаны присоединить теорему Дезарга в качестве новой аксиомы этой плоской геометрии. Затем Гильберт показал, что, исключив "аксиому Дезарга", можно построить новую, так называемую недезар-гову, геометрию на плоскости. Так на протяжении веков раскрывалась чрезвычайно важная роль теоремы Дезарга в проективной геометрии.